-
第三次全国土壤普查 (以下简称“三普”) 是继第二次全国土壤普查43年后对我国土壤的又一次全面体检，对全面掌握我国土壤资源情况，真实准确掌握土壤质量基础状况，确保国家粮食安全具有重大意义[1-2]。土壤检测作为三普数据的核心来源，是成果编制的重要基础，是“全面体检”的重要保障[3-4]。然而，测量由于误差的存在，使得测量结果具有不确定性。1963年，测量不确定度的概念被提出，用于说明测量结果的不确定性[5]，其不关注“真值”的未知性，而是通过定义一个量值区间来表达量值不完整的信息[6]。测量不确定度用于评估定量方法和检测结果的可靠性，是国际社会推荐使用的评价测量活动的重要质量指标[7-9]。测量结果的可靠性很大程度上取决于其不确定度的大小，不确定度越小，说明测量水平越高，测量结果的使用价值越大[10]。为确保三普数据的准确可靠，有必要针对三普的测试指标开展不确定度评定，分析不确定度的关键组成和来源，明确土壤检测的关键点，减小土壤检测结果的不确定性，提高三普数据的质量水平。
目前，有关不确定度的研究论文主要基于不同的检测方法和检测项目开展不确定度评定，以土壤检测为例，如波长色散X射线荧光法测定土壤砷的不确定度评定[11]；电感耦合等离子体质谱法测定土壤金属元素的不确定度评定[12]；电感耦合等离子体发射光谱法测定土壤全钾的不确定度评定[13]等。然而，该类研究主要集中在如何对既定的测试流程开展不确定度评定；对于如何应用不确定度作为分析工具，指导优化样品检测，提高检测结果的质量水平，却鲜有文献报道。
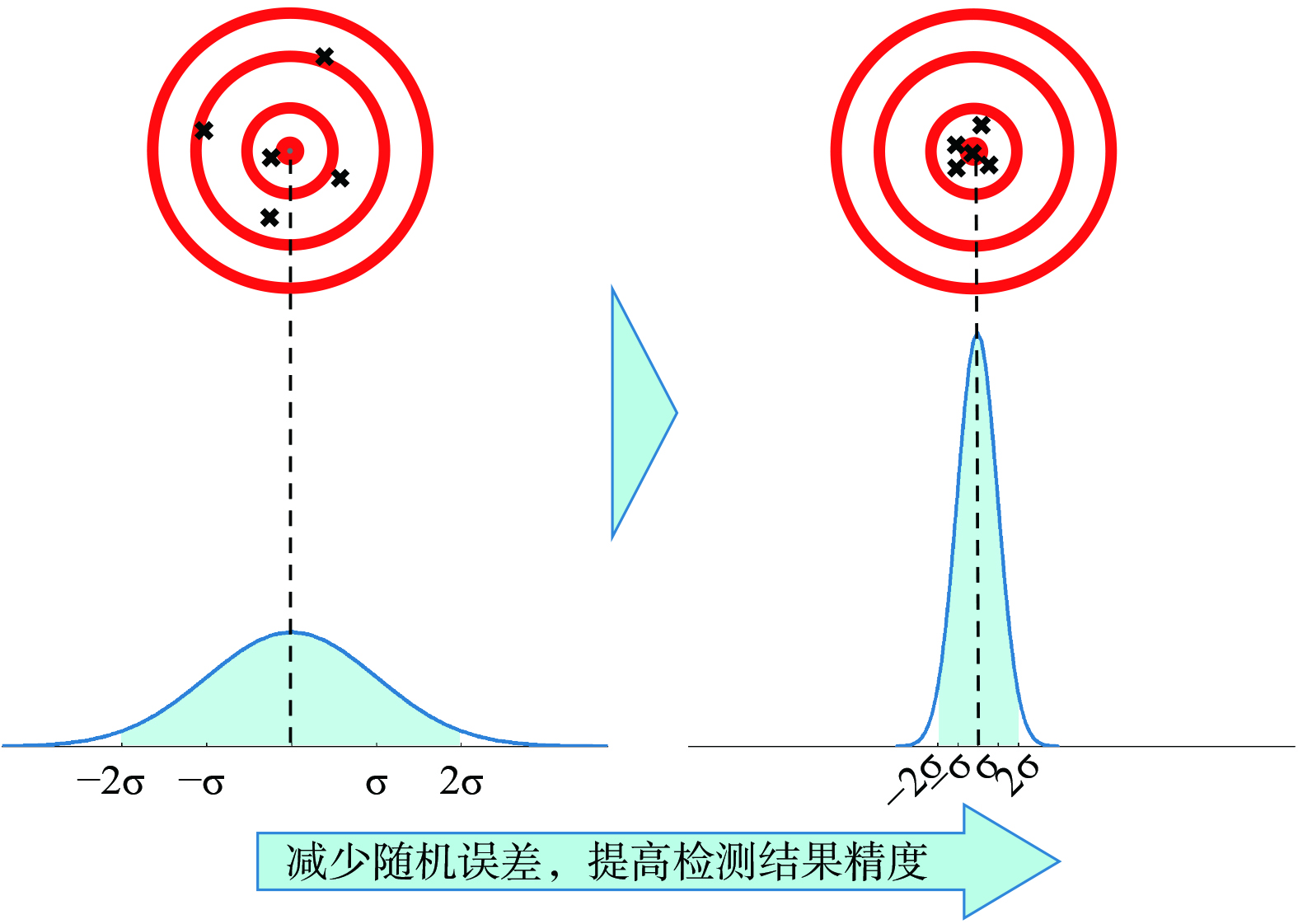
本研究从三普指标中占比最高的土壤微量元素和重金属入手，对ICP-MS法测定土壤总铬、全锰、全铜、全锌、全镍、全钼、总镉和总铅开展不确定度评定，通过分析各指标的关键不确定度分量及其内在规律，研究影响不确定度大小的关键因素，并据此指导检测方法的优化，以期更好的控制不确定度的大小，减小实验结果的分散性，提高检测结果的质量水平，如图1所示。
-
电感耦合等离子体质谱仪 (Agilent
7800 型，安捷伦科技 (中国) 有限公司) ；万分位分析天平 (MS205DU型，瑞士梅特勒-托利多公司) ，微波消解仪 (Mars 6型，美国CEM公司) 。 -
1) 标准品。多元素标准溶液GNM-M2310367-2013，其中锰100 mg·L−1，铬、镍、铜、锌和铅为10.0 mg·L−1，钼和镉为1.0 mg·L−1；内标溶液GNM-M062478-2013，包含铋、锗、铟、镥、铑、钪和铽，质量浓度为10.0 mg·L−1。
2) 试剂。硝酸 (HNO3) 为电子纯；过氧化氢 (H2O2) 、盐酸 (HCl) 和氢氟酸 (HF) 为优级纯。
-
土壤总铬、全锰、全铜、全锌、全镍、全钼、总镉和总铅的测定依据《第三次全国土壤普查技术规程规范》 (修订版) [14]中规定的方法，采用ICP-MS法进行检测。称取过0.149 mm孔径尼龙筛的风干土壤样品0.1 g (精确至0.000 1 g) 于微波消解管中，用少量水润湿并加入4 mL浓硝酸、1 mL浓盐酸、1 mL氢氟酸及1 mL过氧化氢后，进行微波消解，消解后的样品于150 ℃赶酸，至内溶物尽干，最后用纯水转移样品并定容至50 mL，待测。
-
1) 仪器工作。射频发生器功率：1 550 W；雾化室：石英同心雾化器；雾化室温度：2 ℃；雾化气：氩气，流量为1.09 L·min−1；碰撞气：氦气，流量为4.3 L·min−1；采样深度8.0 mm，信号的采集次数3次。
2) 标准工作液。使用2%硝酸配制标准系列工作液，其中锰的质量浓度分别为0、100、200、400、600、800、1 000、1 500、2 000、5 000 μg·L−1；铬、镍、铜、锌和铅的质量浓度分别为0、10、20、40、60、80、100、150、200、500 μg·L−1；钼和镉的质量浓度分别为0、1、2、4、6、8、10、15、20、50 μg·L−1。
3) 样品测定。将质量浓度为500 μg·L−1的内标溶液通过蠕动泵在线加入，先测定系列标准工作液建立标准曲线，再测定样品消解液。
-
土壤金属元素全量按式(1)计算。
式中：w为土壤金属元素的质量分数，mg·kg−1；ρ为试样中待测元素的质量浓度，μg·L−1；V为消解后样品定容体积，mL；m为称取土壤的质量，g；wdm为土壤干物质的质量分数，按式(2)计算，%。
式中：wdm为土壤干物质的质量分数，%；m0为带盖容器的质量，g；m1为带盖容器及风干土壤的总质量，g；m2为带盖容器及烘干土壤的总质量，g。
根据实验方法与数学模型，土壤金属元素测量的主要不确定度来源详见表1。对土壤进行平行双样测定，其中二级分量wA代表平行A样的测定结果，其由标准曲线校正的质量浓度ρA、消解液定容体积V、称取样品质量mA和土壤干物质wdm的4项三级不确定度分量合成得到；平行B样wB与平行A样wA类似。一级分量平均值
$ \bar{w} $ 由二级分量wA和wB合成得到，其与另外两个一级分量测量重复性R和结果值修约RND合成后，得到土壤金属元素w的合成不确定度。 -
1) 质量浓度ρA/ρB。ρA的不确定度来源于标准曲线校正。标准曲线使用线性最小二乘法拟合，最小二乘法拟合的前提是假定横坐标值 (质量浓度ρ) 的不确定度远小于纵坐标值 (仪器响应) 的不确定度，即标准系列工作液的不确定度足够小以致可以忽略[15-16]。ρA的相对标准不确定度 (用urel表示) 见式(3)，其中b为标准曲线的斜率；m为样品测试时的仪器信号采集次数，m=3；n为标准曲线的质量浓度点数与仪器信号采集次数的乘积，n=10×3=30；s为标准曲线的残余标准差。urel(ρB)的计算参考urel(ρA)。
2) 定容体积V。V的相对标准不确定度见式(4)，其中a(V)为定容使用的容量瓶的允差，取值参考《玻璃量具校准规程》 (JJG 196－2006) [17]；α为水体积膨胀系数，取α=2.1×10−4 ℃−1；Δt为实验室环境温度的变化幅度，取Δt=±3 ℃。
3) 称量质量mA/mB。mA的相对标准不确定度见式(5)，其中a(m)为天平允差，对万分之一天平，a(m)=0.5 mg。urel(mB)的计算参考urel(mA)。
4) 土壤干物质wdm。wdm的相对标准不确定度见式(6)，对万分之一天平，a(m)=0.5 mg。
5) 测量重复性R。R的相对标准不确定度见式(7)，采用极差法计算，对于平行双样测定，极差系数C=1.13[18]。
6) 结果值修约RND。RND的相对标准不确定度详见式(8)，其中a为结果值保留位数的修约间隔误差区间的半宽。
-
1) 二级分量平行A样的不确定度合成。平行A样的标准不确定度 (用u表示) 由ρA、V、mA、wdm的相对标准不确定度合成得到，见式(9)。平行B样不确定度合成同平行A样。
2) 一级分量平均值
$ \bar{w} $ 的不确定度合成。平均值$ \bar{w} $ 的相对标准不确定度由wA和wB的标准不确定度合成得到，见式(10)。3) 土壤金属元素w合成不确定度。土壤金属元素w的相对合成标准不确定度 (用ucrel表示) 由平均值
$ \bar{w} $ 、测量重复性R和结果值修约RND的相对标准不确定度合成得到，见式(11)。根据w的相对合成标准不确定度ucrel(w)，可计算w的合成标准不确定度uc(w)和扩展不确定度U(w)，见式(12)和式(13)，其中扩展不确定度U(w)中的k=2，提供大约95%的置信概率。
对实际测试的土壤样品开展不确定度评定，不确定度计算过程中主要的数据列于表2中。
-
根据式(9)和式(10)，将wA、wB和
$ \bar{w} $ 的计算式代入式(11)，可得到式(14)如下。根据式(14)，
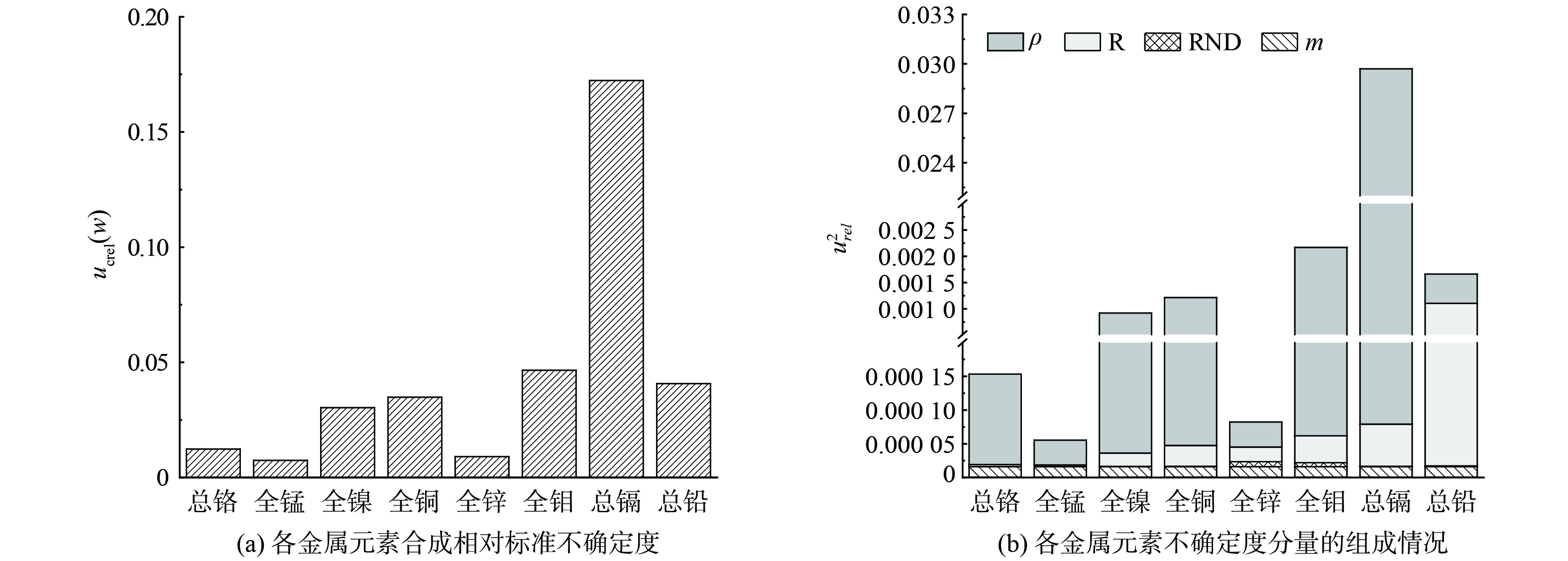
$ {{u}}_{\text{c}\text{rel}}^{\text{2}}\left({w}\right) $ 由10项不确定度分量组成，包括8项三级分量ρA/B、V、mA/B和wdm，2项一级分量R和RND，将10项不确定度分量进行归一化处理[19]并参考表1不确定度分量的拆解方法作图，如图2所示。图2展示了不同金属元素测量中，各项不确定度分量的占比情况，可见不同金属元素不确定度分量的占比情况并不一致，但主要的不确定度分量均集中在质量浓度ρ和测量重复性R这2项。比较各指标合成相对标准不确定度ucrel(w)及其不确定度分量
$ {{u}}_{\text{c}\text{rel}}^{\text{2}} $ 的组成，如图3所示。从图3(a)可见，各金属元素的合成相对标准不确定度大小不一，其中总镉最大，全锰最小，分析其中不确定度分量的组成情况，如图3(b)，可见总镉和全锰合成相对标准不确定度的差异，主要体现在不确定度分量ρ和R的差异上，ρ和R越大，导致不确定度越大，因此ρ和R是影响不确定度大小的关键分量。其他的不确定度分量如称样量m，与称量天平的精度和称样量的大小有关，从图3(b)中可见，各金属元素中不确定度分量m的大小不变，当合成不确定度较小时，会导致其在合成不确定度中的占比提高 (如图2(b)和图2(e)) ，反之则占比降低，但由于其不确定度较小 (本例中计算得到的ucrel(m)以百分数计仅约0.4%) ，其对合成不确定度的影响十分有限。 -
待测元素质量浓度ρ的不确定度来源于标准曲线的校正，根据标准曲线的线性范围，计算不同质量浓度下的标准不确定度及相对标准不确定度，并作图，如图4所示。图4以总铬为例，随着质量浓度的增加，铬的标准不确定度u(ρ)随着质量浓度的升高，呈先下降再升高的趋势，u(ρ)在100~200 μg·L−1间最低；而相对标准不确定度urel(ρ)则随着质量浓度的升高而不断降低，在质量浓度最高点时最低。根据式(9)，wA的不确定度由urel(ρA)合成得到，因此当质量浓度值越接近标准曲线最高点，urel(ρ)越低，此时合成得到的urel(w)越低。对于标准曲线校正，目前普遍认为在曲线中间点附近的质量浓度最准确，也有文献建议尽量使待测元素的质量浓度位于标准曲线的中间位置[20-21]。从标准不确定度u(ρ)的角度来说，这是一个正确的判断，而从减小检测结果不确定度的角度出发，由于w并非由u(ρ)而是由urel(ρ)合成得到，因此应尽量使待测元素的质量浓度位于标准曲线的最高点附近，而非中间点附近。
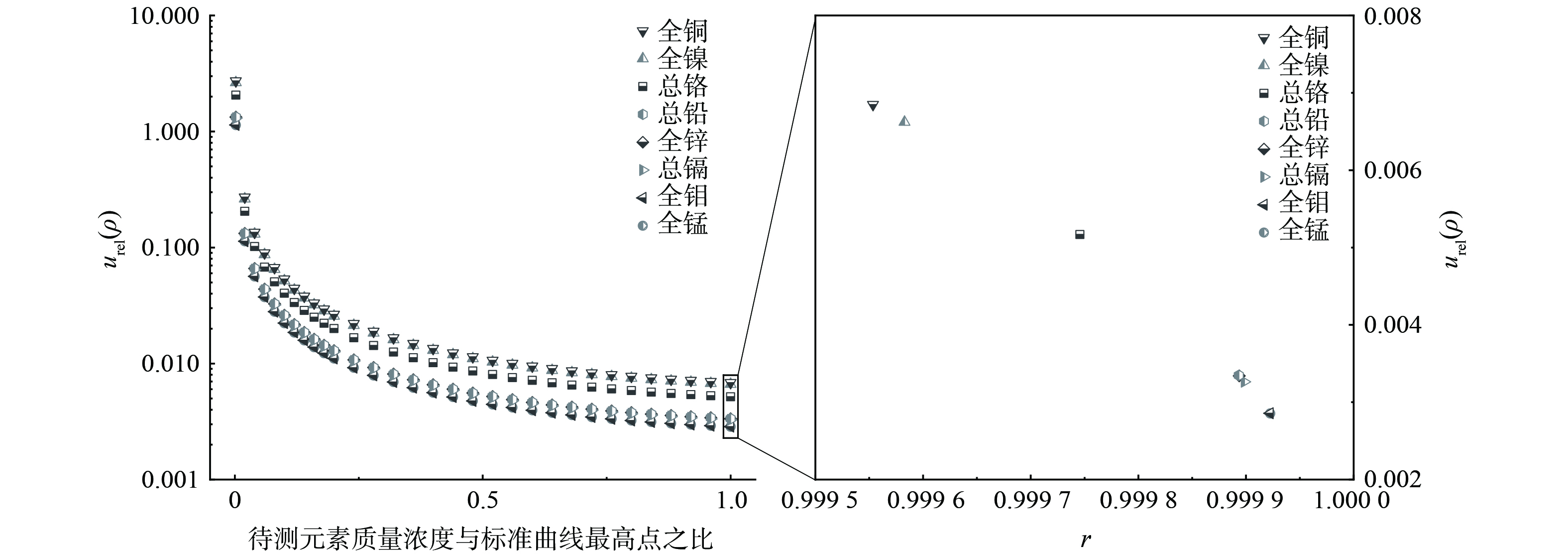
图5展示了不同金属元素间urel(ρ)的关系，在相同比值 (待测元素的质量浓度与标准曲线最高点的比值) 下，urel(ρ)从大到小排列为全铜>全镍>总铬>总铅>总锌>总镉>全钼>全锰，结合标准曲线的r值可知，urel(ρ)与r值成反比关系，r值越接近1，urel(ρ)越低。r为相关系数，r越接近1，代表因变量和自变量的相关性越好，因此通过标准曲线计算得到的结果的不确定度也越小。
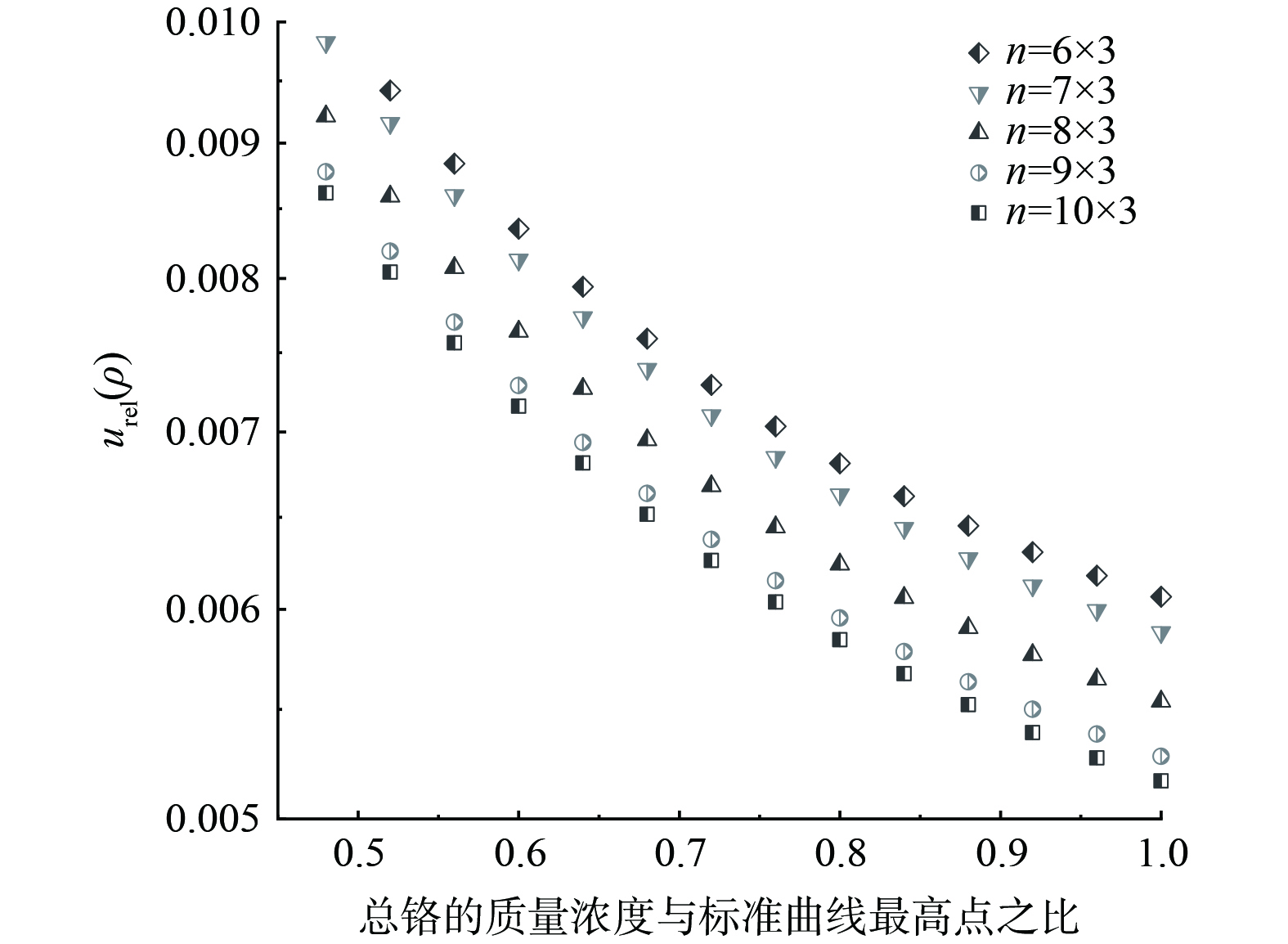
此外，根据式(3)，n与urel(ρ)成反比，n为标准曲线的质量浓度点数与仪器信号采集次数的乘积，即增加标准曲线的点数或增加仪器信号采集次数，可以降低urel(ρ)。图6以总铬为例，展示了不同n值下的相对标准不确定度，可见n越大，urel(ρ)越小。
综上，要控制减小待测元素质量浓度ρ的相对标准不确定度urel(ρ)，在测试的过程中应关注以下3点。
1) 合理设置标准曲线最高点，使消解液的待测金属元素浓度尽可能接近最高点。
2) 标准曲线的相关系数r尽可能接近1。
3) 使用更多的质量浓度点建立标准曲线，以及增加仪器信号采集次数。
-
测量重复性的不确定度依据式(7)计算，对于平行双样，一般使用相对偏差 (RD) 计算精密度，结合式(7)，可通过RD计算urel(R)，如式(15)所示。
可见，相对偏差越大，urel(R)越大。根据式(15)，相对偏差每增大1%，相对标准不确定度urel(R)增大约1.25%，当相对偏差达到8%时，urel(R)达到10%。因此，提高测量精密度，同样是降低土壤金属元素测量不确定度的关键的因素。但值得注意的是，相比于标准曲线校正引入的不确定度可以通过测量程序优化，对于精密度的提高，更考验实验室对环境条件的控制和实验人员技术水平的高低。此外，精密度也反映了样品本身的均匀性情况。
-
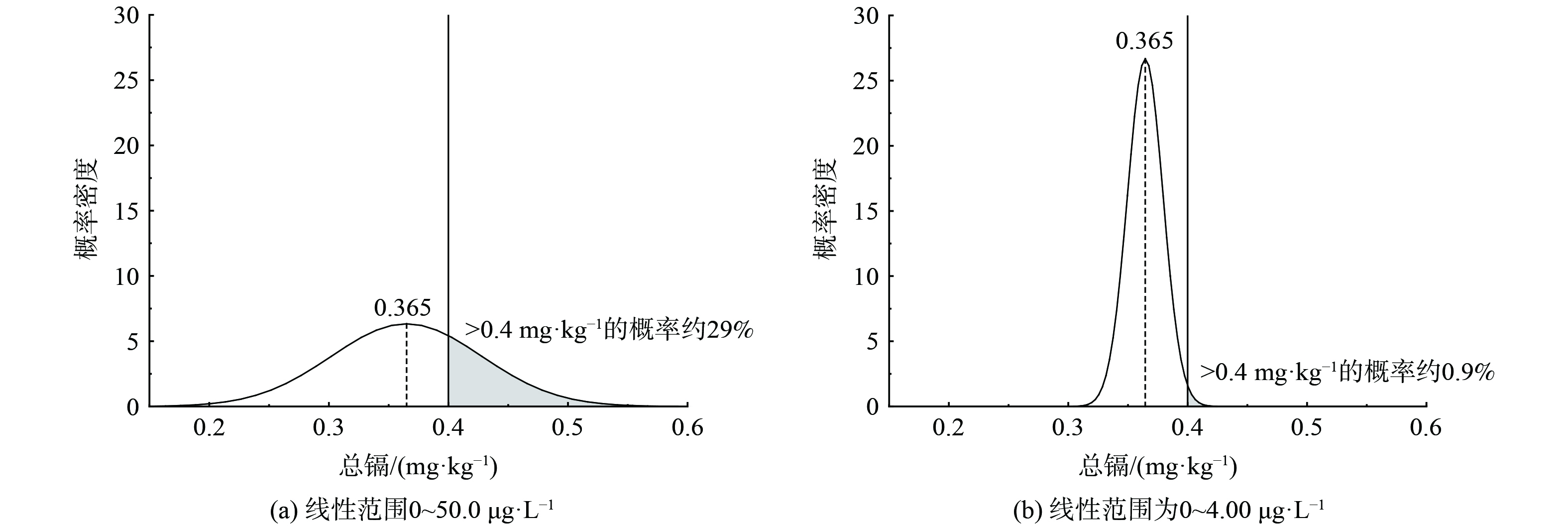
本研究测得土壤镉的质量分数为0.365 mg·kg−1，扩展不确定度U(w)=0.126 mg·kg−1 (k=2) ，根据《土壤环境质量 农用地土壤污染风险管控标准 (试行) 》 (GB 15618-2018) [22]，水田镉在5.5<pH≤6.5范围时的筛选值为0.4 mg·kg−1。根据《判定规则和符合性声明指南》 (CNAS-GL015: 2022) [23]，在进行合格评定时，需要考虑不确定度的影响。当土壤镉浓度为 (0.365±0.126) mg·kg−1 (k=2)时，虽然0.365 mg·kg−1的结果小于筛选值0.4 mg·kg−1，但结合不确定度后，其浓度区间在0.239~0.461 mg·L−1 (95%置信限) 范围内，由于有部分范围超过了0.4 mg·kg−1，此时无法对其进行合格评价，或者说评价为合格时，误判的概率超过5% (按正态分布，误判的概率约29%) ，具有较大的误判风险。从另一个角度解释，如在此不确定度下分别进行10次样品检测，将出现3个超标结果和7个合格结果。可见，不确定度的大小体现了检测结果质量水平的高低，特别是当结果接近标准筛选值时，不确定度的大小将直接影响合格评价。
从图3(b)可见，本文案例中土壤镉的主要不确定度分量为质量浓度ρ，其原因在于土壤消解液的镉浓度较低，仅约0.17 μg·L−1，而标准曲线的线性范围为0~50.0 μg·L−1，由此导致了ρ的相对标准不确定度较高。通过移除镉的标准曲线中浓度较高的点，调整线性范围至0~4.00 μg·L−1，重新计算不确定度，得到结果为 (0.365±0.030) mg·kg−1 (k=2)，即镉的结果在0.335~0.395 mg·L−1 (95%置信限) 范围内，此时评价镉的结果为合格，其概率>95%，误判概率<5%。图7展示了不确定度优化前后镉的不确定度范围，对比原来的不确定度，优化后的不确定度更小，数据更集中，此时镉浓度>0.4的概率仅约0.9%，即评价镉为合格的概率>99%，对比原来的评价，此时的评价更准确可靠。
综上所述，在进行土壤金属检测时，线性范围的设置十分关键，合适的线性范围能很大程度减小土壤金属元素测量结果的不确定度。特别是对于有标准筛选值的土壤金属元素，如GB 15618-2018中的铬、镍、铜、锌、镉和铅，标准曲线的浓度范围可根据筛选值的大小进行设置，这对目标元素质量分数位于筛选值附近的样品，能进行更准确可靠的评价。表3给出当土壤称样量为0.1 g，定容体积为50 mL，采用ICP-MS法测定时，各金属元素合适的标准曲线最高点质量浓度的设置，在实际的土壤检测过程中，实验室应根据自身情况设置合适的线性范围。
-
1) 对土壤金属元素开展测量不确定度评定，其中的关键不确定度分量为消解液的质量浓度ρ和测量重复性R，减小上述2项不确定度分量的大小，能有效减小土壤金属元素的测量不确定度。
2) 不确定度分量ρ来源于标准曲线校正，要控制减小ρ的相对标准不确定度，一是合理设置标准曲线最高点，使得待测消解液的浓度尽可能接近最高点；二是尽量使用相关系数r值较高的标准曲线；三是使用更多的数据点建立标准曲线，以及增加仪器信号采集次数。
3) 不确定度分量R受测量精密的影响，相对偏差每增大1%，R的相对标准不确定度增大约1.25%，因此，提高测量精密度，能够有效降低不确定度分量R。
4) 测量不确定度的大小体现了检测结果质量水平的高低，特别是当结果接近标准筛选值时，具有较大的误判风险；减小测量不确定度，能够使测量结果的离散程度更小，增加合格评价时的准确性和可靠性。
土壤金属元素测量结果的不确定性与其关键影响因素
Uncertainty in soil metal element measurements and its key influencing factors
-
摘要: 土壤检测是第三次全国土壤普查数据的核心来源，而由于测量误差的存在，导致测量结果具有不确定性，并影响结果的可靠性。为提高检测结果的质量水平，选取普查中的总铬、全锰、全铜、全锌、全镍、全钼、总镉和总铅指标开展不确定度评定，研究影响不确定度大小的关键因素。结果表明，土壤金属元素测量的关键不确定度分量来源于消解液的质量浓度ρ和测量重复性R。减小ρ引入的不确定度可通过设置合理的标准曲线线性范围，使ρ尽可能接近曲线最高点；使用相关系数r值高的标准曲线；使用更多的质量浓度点建立标准曲线和增加仪器信号采集次数等方法。减小R引入的不确定度可通过提高测量精密度。通过优化，土壤总镉的不确定度范围由 (0.365±0.126) mg·kg−1 (k=2) 降低至 (0.365±0.030) mg·kg−1 (k=2) ，对于0.4 mg·kg−1的筛选值，不确定度的减小使土壤总镉在进行合格评价时得到更准确可靠的结果。该研究结果阐明了影响土壤金属元素测量的关键不确定度分量，为实验室有效控制土壤金属元素的测量不确定度，减小检测结果的分散性，提高检测结果的质量水平提供了理论参考。Abstract: Soil testing is the cornerstone of data for the Third National Soil Condition Census. However, the presence of measurement errors introduces uncertainty and affects the reliability of the results. To enhance the quality of testing outcomes, an evaluation of uncertainty was conducted for total chromium, manganese, copper, zinc, nickel, molybdenum, cadmium and lead in the survey, focusing on the factors that influence the magnitude of uncertainty. The findings indicated that the key components of uncertainty in soil metals measurements stem from the mass concentration of the digestion solution (ρ), and the measurement repeatability (R). The uncertainty introduced by ρ could be reduced by appropriate establishing a linear range for the standard curve to ensure that ρ was as close as possible to the highest point of the curve; using a standard curve with a higher Pearson correlation coefficient (r); employing more mass concentration points to establish standard curves and increasing the number of instrument signal acquisitions. The uncertainty introduced by R could be reduced by improving measurement precision. Through optimization, the uncertainty range for total cadmium was reduced from (0.365±0.126) mg·kg−1 (k=2) to (0.365±0.030) mg·kg−1 (k=2). For the screening value of 0.4 mg·kg−1, the reducing uncertainty led to more accurate and reliable results in the conformity assessment of total cadmium in soils. This study clarified the key components of uncertainty affecting the measurement of soil metals, providing a theoretical reference for laboratories to effectively control the measurement uncertainty of soil metals, reduce the dispersion of test results, and enhance the quality level of the outcomes.
-
-
图 1 减小不确定度以提高土壤金属元素检测结果的质量水平
Figure 1. Reduce uncertainty to improve the quality of soil metal elements test
图 2 土壤不同金属元素不确定度分量的拆解及其占比
Figure 2. Deconstruction of uncertainty components and their percentages of different metal elements in soil
图 3 土壤不同金属元素合成相对标准不确定度及其不确定度分量
Figure 3. Combined relative standard uncertainties and their uncertainty components of different metal elements in soil
图 4 总铬在不同质量浓度下的标准不确定度与相对标准不确定度
Figure 4. Standard uncertainties and relative standard uncertainties of total chromium at different mass concentrations
图 5 土壤不同金属元素的相对标准不确定度
Figure 5. Relative standard uncertainties of different metal elements in soil
图 6 总铬标准曲线在不同n值下的相对标准不确定度
Figure 6. Relative standard uncertainties of total chromium standard curves at different values of n
图 7 总镉线性范围调整前后的不确定度范围的变化
Figure 7. Change in uncertainty range before and after linear range adjustment for total cadmium
表 1 土壤金属元素不确定度分量的拆解
Table 1. Deconstruction of uncertainty components for soil metal elements
合成
不确定度一级不确定度
分量二级不确定度
分量三级不确定度分量 土壤金属
元素w平均值 $ \bar{w} $ 平行wA 标准曲线校正的
质量浓度ρA消解液定容体积V 称取样品质量mA 土壤干物质wdm 平行wB 标准曲线校正的
质量浓度ρB消解液定容体积V 称取样品质量mB 土壤干物质wdm 测量重复性R — — 结果值修约RND — — 
下载: 导出CSV
表 2 土壤金属元素不确定度计算过程中的主要数据
Table 2. Main data in the process of calculating the uncertainty of soil metal elements
金属
元素平行 urel(ρ) urel(V) urel(m) urel(wdm) urel(w) u(w)/
(mg·kg−1)u( $ \bar{w} $
(mg·kg−1)urel( $ \bar{w} $ urel(R) urel
(RND)$ \bar{w} $
(mg·kg−1)ucrel(w) uc(w)/
(mg·kg−1)U(w)/
(mg·kg−1)总铬 A 1.154×10−2 5.468×10−4 3.918×10−3 5.572×10−4 1.221×10−2 1.029 1.03 1.23×10−2 1.75×10−3 3.43×10−4 84.2 1.24×10−2 1.0 2.0 B 1.162×10−2 5.468×10−4 3.937×10−3 5.572×10−4 1.230×10−2 1.034 全锰 A 6.044×10−3 5.468×10−4 3.918×10−3 5.572×10−4 7.245×10−3 6.458 6.47 7.27×10−3 1.57×10−3 3.24×10−4 890 7.44×10−3 7 14 B 6.086×10−3 5.468×10−4 3.937×10−3 5.572×10−4 7.290×10−3 6.482 全镍 A 2.955×10−2 5.468×10−4 3.918×10−3 5.572×10−4 2.982×10−2 1.250 1.25 3.00×10−2 4.44×10−3 6.91×10−4 41.8 3.03×10−2 1.3 2.6 B 2.991×10−2 5.468×10−4 3.937×10−3 5.572×10−4 3.017×10−2 1.256 全铜 A 3.393×10−2 5.468×10−4 3.918×10−3 5.572×10−4 3.416×10−2 1.292 1.30 3.44×10−2 5.56×10−3 7.67×10−4 37.7 3.49×10−2 1.3 2.6 B 3.440×10−2 5.468×10−4 3.937×10−3 5.572×10−4 3.464×10−2 1.299 全锌 A 6.062×10−3 5.468×10−4 3.918×10−3 5.572×10−4 7.260×10−3 0.764 9 0.766 7.29×10−3 4.64×10−3 2.75×10−3 105 9.07×10−3 1 2 B 6.130×10−3 5.468×10−4 3.937×10−3 5.572×10−4 7.327×10−3 0.7662 全钼 A 4.603×10−2 5.468×10−4 3.918×10−3 5.572×10−4 4.620×10−2 5.457×10−2 5.47×10−2 4.61×10−2 6.31×10−3 2.43×10−3 1.19 4.66×10−2 0.06 0.12 B 4.579×10−2 5.468×10−4 3.937×10−3 5.572×10−4 4.596×10−2 5.484×10−2 总镉 A 0.172 8 5.468×10−4 3.918×10−3 5.572×10−4 0.172 8 6.260×10−2 6.28×10−2 0.172 7.90×10−3 7.92×10−4 0.365 0.172 0.063 0.126 B 0.171 4 5.468×10−4 3.937×10−3 5.572×10−4 0.171 5 6.290×10−2 总铅 A 2.417×10−2 5.468×10−4 3.918×10−3 5.572×10−4 2.450×10−2 0.639 1 0.641 2.39×10−2 3.30×10−2 1.08×10−3 26.8 4.08×10−2 1.1 2.2 B 2.303×10−2 5.468×10−4 3.937×10−3 5.572×10−4 2.337×10−2 0.642 7
下载: 导出CSV
表 3 土壤金属元素标准曲线最高点质量浓度的设置
Table 3. Mass concentration setting of the highest point of the soil metal element standard curve
金属元素 标准曲线最高点质量浓度/ (μg·L−1) pH≤5.5 5.5<pH≤6.5 6.5<pH≤7.5 pH>7.5 镉 水田 0.8 1.0 1.5 2.0 其他 0.8 0.8 0.8 1.5 铅 水田 200 250 350 600 其他 175 225 300 425 铬 水田 625 625 750 875 其他 375 375 500 625 铜 果园 375 375 500 500 其他 125 125 250 250 镍 150 175 250 475 锌 500 500 625 750
下载: 导出CSV
-
[1] 陈春秀, 阳路芳, 雷建容, 等. 关于做好第三次全国土壤普查内业质控的几点思考[J]. 中国农业综合开发, 2023(8): 16-17. [2] 郝士横, 吴香源, 吴克宁. 科学施策、问计大地——浅论做好第三次全国土壤普查的四要素[J]. 中国农业综合开发, 2024(2): 34-36. [3] 全国土壤普查办内业工作组. 全国土壤普查内业工作2023年重点任务[J]. 中国农业综合开发, 2023(4): 15-17. [4] 李琪, 李继福, 巩细民, 等. 抓牢检测环节 打好成果基础 湖北省第三次土壤普查试点内业测试经验分享[J]. 中国农业综合开发, 2024(4): 21-23. [5] 倪育才. 实用测量不确定度评定[M]. 5版. 北京: 中国质检出版社, 2006: 3. [6] 张诗诗, 王薇, 赵海建, 等. 临床化学检验中精密度、正确度、总误差和测量不确定度的讨论[J]. 临床检验杂志, 2017, 35(9): 641-643. [7] 陆明, 范国荣, 汪杨, 等. 测量不确定度在药品领域的应用[J]. 医药导报, 2013, 32(8): 1053-1057. doi: 10.3870/yydb.2013.08.027 [8] 王丽楠, 杨美华, 陈建民. 不确定度分析在药物研究中的应用[J]. 中草药, 2008, 39(3): 464-467. doi: 10.3321/j.issn:0253-2670.2008.03.046 [9] 陆明, 范国荣, 汪杨, 等. 测量不确定度在药品检测领域的研究进展[J]. 中国药事, 2013, 27(5): 485-492. doi: 10.3969/j.issn.1002-7777.2013.05.010 [10] 丁海峰, 姚尧, 张琪, 等. 医学实验室目标测量不确定度的选择[J]. 数理医药学杂志, 2023, 36(10): 762-767. doi: 10.12173/j.issn.1004-4337.202309069 [11] 杨永建, 夏莎莎, 李红华, 等. 波长色散X射线荧光法测定土壤中的砷及不确定度评定[J]. 环境工程学报, 2024, 18(2): 609-613. doi: 10.12030/j.cjee.202312026 [12] 陈灿, 刘慧娟, 曹俊, 等. 响应面法优化土壤和沉积物中多种金属元素测定及其不确定度评定[J]. 环境污染与防治, 2022, 44(9): 1142-1147. [13] 张丽萍, 王久荣, 许丽卫, 等. 电感耦合等离子体发射光谱法测定土壤全钾不确定度的评定与表示[J]. 中国土壤与肥料, 2021(2): 343-347. doi: 10.11838/sfsc.1673-6257.20068 [14] 国务院第三次全国土壤普查领导小组办公室. 第三次全国土壤普查技术规程规范(修订版)[EB/OL]. [2024-05-29]. http://www.moa.gov.cn/ztzl/dscqgtrpc/zywj/202307/P020230720371072116980.pdf. [15] Ellison S, Williams A. Eurachem/CITAC guide: quantifying uncertainty in analytical measurement[M]. 3rd Edition. ISBN: 978-0-948926-30-3. 2012: 76-77. [16] 中国合格评定国家认可委员会. 化学分析中不确定度的评估指南: CNAS-GL-006: 2019[S/OL]. [2024-05-29]. https://www.cnas.org.cn/images/rkgf/sysrk/rkzn/2019/04/18/84DF453E2EE8DB5F212967680DA1A89A.pdf. [17] 全国流量容量计量技术委员会. 玻璃量具校准规程: JJG 196-2006[S]. 北京: 国家质量监督检验检疫总局, 2006. [18] 全国法制计量管理计量技术委员会. 测量不确定度评定与表示: JJF 1059.1-2012[S]. 北京: 国家质量监督检验检疫总局, 2012. [19] 林健辉, 卢嘉慧, 吴欣颖, 等. 受控堆肥条件下可降解材料最终需氧生物分解能力测定的不确定度评定研究[J]. 中国塑料, 2022, 36(9): 140-147. [20] 卢秋, 姚苏芝, 梁晓曦, 等. 电感耦合等离子体质谱法测定固体废物中镉的不确定度评定[J]. 化学分析计量, 2024, 33(3): 115-120. doi: 10.3969/j.issn.1008-6145.2024.03.020 [21] 朱叶萌, 黎雄才, 王刚. 火焰原子吸收光谱法测定配合饲料中铜、铁和锰含量的不确定度评定[J]. 饲料工业, 2024, 45(9): 115-120. [22] 生态环境部, 国家市场监督管理总局. 土壤环境质量 农用地土壤污染风险管控标准(试行): GB 15618-2018[S]. 北京: 中国环境出版集团, 2018. [23] 中国合格评定国家认可委员会. 判定规则和符合性声明指南: CNAS-GL015: 2022[S/OL]. [2024-05-29]. https://www.cnas.org.cn/images/rkgf/sysrk/rkzn/2022/01/20/1642668363321027957.pdf. -
点击查看大图
计量
- 文章访问数: 837
- HTML全文浏览数: 837
- PDF下载数: 26
- 施引文献: 0
