-
改革开放以来,中国经济快速发展,工业化与城镇化不断推进。与此同时,也消耗了大量的能源,而以煤炭为主的能源消费结构使得大气污染物和CO.*?>=>2排放不断增加,许多城市频频出现重度雾霾等恶劣天气,严重危害到经济生产与人们生活。为了降低大气污染物和CO.*?>=>2排放,近年来,中国政府采取强化责任主体的节能减排降碳责任、推进产业结构和能源结构调整以及蓝天保卫战等一系列措施,取得了很好的效果。根据《2018年中国生态环境状况公报》,2018年338个地级及以上城市平均优良天数比例为79.3%,同比上升1.3个百分点。根据中国在波兰卡托维兹《联合国气候变化框架公约》第二十四次缔约方会议(COP24)上公开的数据,到2017年年底,中国单位GDP的CO.*?>=>2排放比2005年下降了46%,超额完成2009年哥本哈根气候大会上提出的下降40%~45%的目标。尽管中国环境治理取得了显著的成绩,但是也应看到,中国仍然面临着较大的节能减排降碳压力,如何进一步降低大气污染物排放,全面改善大气环境质量,完成2030年能源消费总量控制在60亿t标准煤以内、单位国内生产总值CO.*?>=>2排放比2005年下降60%~65%等目标,对中国经济绿色、可持续、高质量发展至关重要。
大气污染物排放和CO.*?>=>2排放具有同步、同源性[1],它们都主要来源于化石燃料燃烧,节约能源尤其是减少化石能源使用可以同时实现大气污染物和CO.*?>=>2减排。2015年修订的《大气污染防治法》、《“十三五”控制温室气体排放工作方案》和《“十三五”生态环境保护规划》等均提出了节能、减排和降碳工作的协同化,许多学者也对能耗、大气污染物和CO.*?>=>2排放之间的关系展开研究。在节能与减排的协同效应方面,BOLLEN et al[2]认为全球能源安全政策在减少大气污染物的同时亦可减少CO.*?>=>2排放;HASANBEIGI et al[3]分析得出节能政策可以促进山东省工业部门PM.*?>=>2.5和SO.*?>=>2的减排;郑季良等[4]测算了宝钢公司的节能减排协同效应。在节能与降碳的协同效应方面,LEE et al[5]基于22座亚洲主要城市的CO.*?>=>2排放量及能耗关系的研究认为提高能效是降低碳排放、实现协同效益的有效手段;刘强等[6]对中国重点区域煤炭消费总量控制政策的碳排放效果进行测算;宋杰鲲等[7]基于VAR模型得出山东省能耗和碳排放具有长期单向Granger因果关系与短期的相互影响;JIANG et al[8]对中国大型商业建筑因节能政策而带来的碳减排效益进行测算。XUE et al[9]的研究表明中国的风电企业电力生产可以降低CO.*?>=>2和大气污染物排放。在减排和降碳的协同效应方面,MCCOLLUM et al[10]基于MESSAGE评估模型指出全球协调一致的脱碳努力可以改善空气质量;WAGNER et al[11]基于构建的GAINS模型对《京都议定书》附件一的国家分析得到温室气体减排措施对大气污染物减排具有协同效应;SHRESTHA et al[12]应用地区长期能源系统模型研究得出泰国电力、工业与交通部门在碳减排的同时也可以降低大气污染物排放;GROOSMAN et al[13]分析了美国的气候政策对大气污染物减排的影响;周颖等[14]分析了中国水泥行业主要污染物和CO.*?>=>2之间的减排协同度;王珍等[15]应用长江经济带11个省市的面板数据说明PM.*?>=>2.5浓度和CO.*?>=>2减排量之间存在显著的协同减排效应;DONG et al[16]基于LMDI分解技术获得单位CO.*?>=>2排放对PM.*?>=>2.5的影响并对中国各省数据进行测算;JIANG et al[17]分析了对沈阳铁西区和上海宝山区温室气体减排对空气污染降低所产生的协同效益进行测算;李丽平等[18-19]分析了“十一五”期间攀枝花市和湘潭市的大气污染物减排措施对碳减排的协同效应。文献梳理表明,无论是全球或国家还是地区或行业、企业,节能、减排和降碳之间均存在着一定的协同效应。但是,当前鲜有文献直接对中国国家层面的节能、减排和降碳之间的协同效应开展定量研究。而这种研究是必要的,它可以帮助中国政府综合考虑三者的内在关系,科学制定节能、减排、降碳目标,实现三者协同优化。基于这一目的,本文运用计量经济分析方法,对中国的能耗、大气污染物排放总量与碳排放强度之间的关系进行定量测度。
全文HTML
-
考虑到数据可获得性、样本时效性及计量分析所需时间序列长度不低于17的基本要求,以2000~2017年为时间区间所涉及的样本数如下。
1)历年的能耗强度,即单位GDP的能源消费总量,用以反映能耗状况。GDP和能源消费总量数据均来源于2018年《中国统计年鉴》,为了消除价格因素的影响,利用GDP平减指数将2000到2016年的GDP数值换算为2000年可比价下的数值。
2)煤炭消费比例即煤炭占能源消费总量的比例,用以反映能耗结构。历年数据均来源于2018年《中国统计年鉴》。
3)SO.*?>=>2排放量,用以反映大气污染物排放状况。2000年、2001~2015年数据分别来源于2000年全国环境统计公报和2018年《中国环境统计年鉴》,2016年和2017年数据分别来源于2017年和2018年《中国统计年鉴》。
4)CO.*?>=>2排放强度,用以反映碳排放状况,应用历年的CO.*?>=>2排放量除以2000年可比价下的GDP测算得到。CO.*?>=>2排放量根据《2006年IPCC国家温室气体清单指南》进行测算[20]包括来源于终端能源消耗的CO.*?>=>2排放量,火力发电和供热加工转换中能源消耗产生的CO.*?>=>2排放量及水泥、玻璃和粗钢等工业产品生产形成的CO.*?>=>2排放量。终端能源消耗量、火力发电和供热加工转换的能源消耗量来源于2014~2018年《中国能源统计年鉴》;水泥、玻璃和粗钢的产量来源于2001~2018年《中国统计年鉴》。
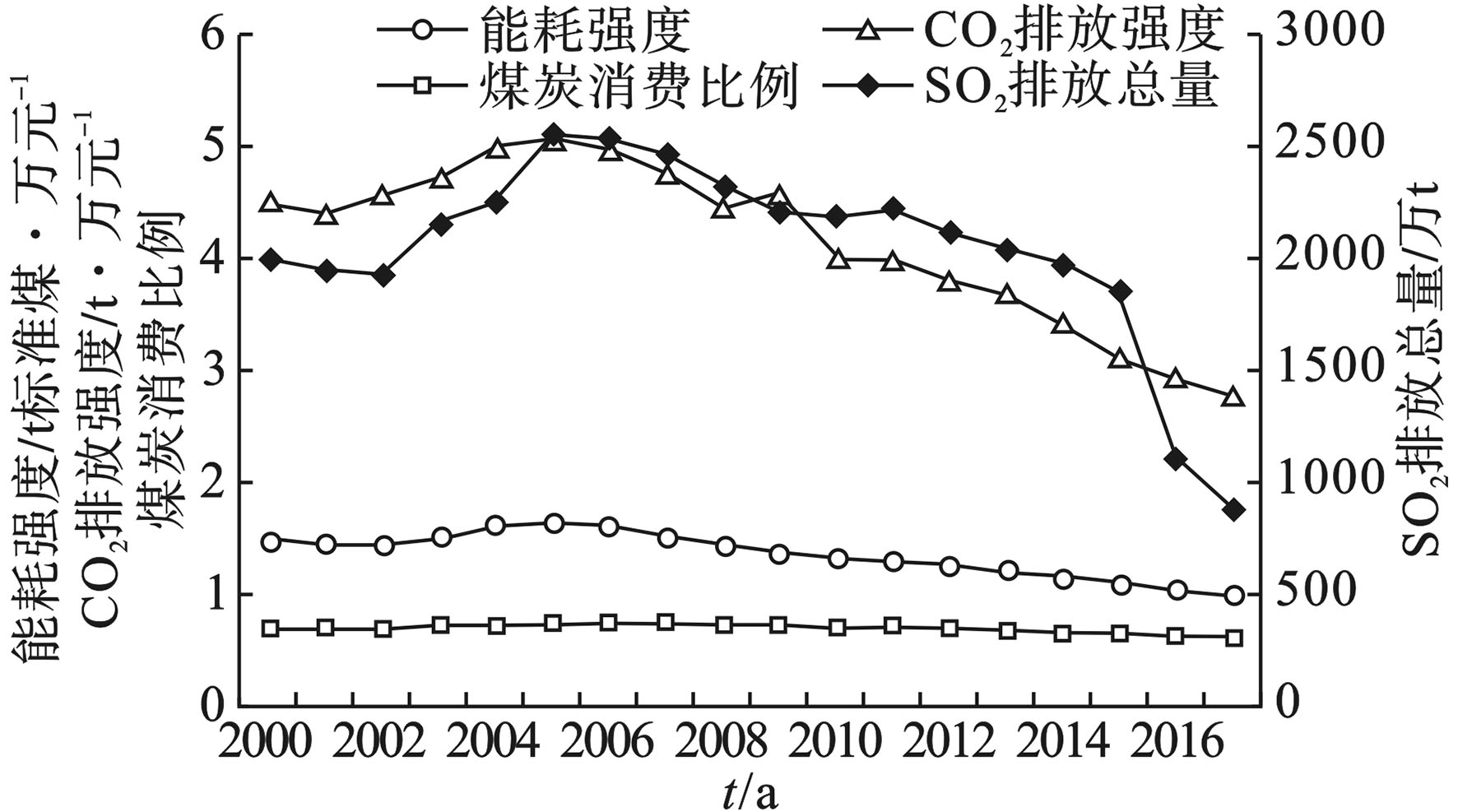
2000~2017年能耗强度、煤炭消费比例、SO.*?>=>2排放量和CO.*?>=>2排放强度的变动情况见图1。
图1可知,4个指标的数据变动情况基本一致。
-
根据学者们的研究成果和中国2000~2017年各指标数据的变动趋势,对中国节能、减排和降碳之间的协同效应提出如下假设:节能、能耗结构优化均对减排、降碳具有协同效应;减排对降碳具有协同效应。以能耗强度、能源消费比例分别表征能耗的强度和结构,SO.*?>=>2排放量、CO.*?>=>2排放强度分别表征大气污染物排放、碳排放,并依次用符号ei、cr、se、ci表示。基于上述假设,构建变量间的基本关系式如:①ci=f.*?>=>1(ei,cr,se);②se=f.*?>=>2(ei,cr)。
为了消除变量间可能存在的异方差,反映变量间的弹性关系,对各变量取自然对数,有节能、能耗结构优化、减排对降碳的协同效应测度模型为:
式(1)中:c.*?>=>1表示常数项,ε.*?>=>1表示随机误差;a.*?>=>1、a.*?>=>2、a.*?>=>3分别表示能耗强度、煤炭消费比例和SO.*?>=>2排放量对于CO.*?>=>2排放强度的弹性系数,即两边分别对ei、cr和se求偏导数,见式(2~4)。
节能、能耗结构优化对减排的协同效应测度模型见式(5)。
式(5)中:c.*?>=>2表示常数项,ε.*?>=>2表示随机误差;b.*?>=>1、b.*?>=>2分别表示能耗强度、煤炭消费比例对于SO.*?>=>2排放量的弹性系数。
1.1. 数据来源
1.2. 研究方法
-
为了防止“伪回归”,采用ADF单位根检验方法检验时间序列中是否存在单位根,以确定序列的平稳性,结果见表1。
表1可知,经过二阶差分后,4个序列均为平稳序列,表明它们之间可能存在协整关系。
-
为判断不同变量之间的线性组合即模型(1)和模型(5)是否平稳,对变量组合进行基于向量自回归模型VAR(p)的协整检验。计算得到组合(Lnci、Lnei、Lnc和Lnse)对应不同VAR滞后阶数的各准则数值见表2。
表2可知,按照LR、FPE、AIC、SC和HQC等准则,最佳滞后阶数p均为2。
基于VAR(2)模型进行Johansen协整检验,得到迹统计检验结果和最大特征根统计检验结果见表3。
表3可知,无论是迹统计检验还是最大特征根检验均表明4个变量之间存在着长期协整关系。
同时得到Lnci、Lnei、Lncr和Lnse之间的协整方程为(6)。
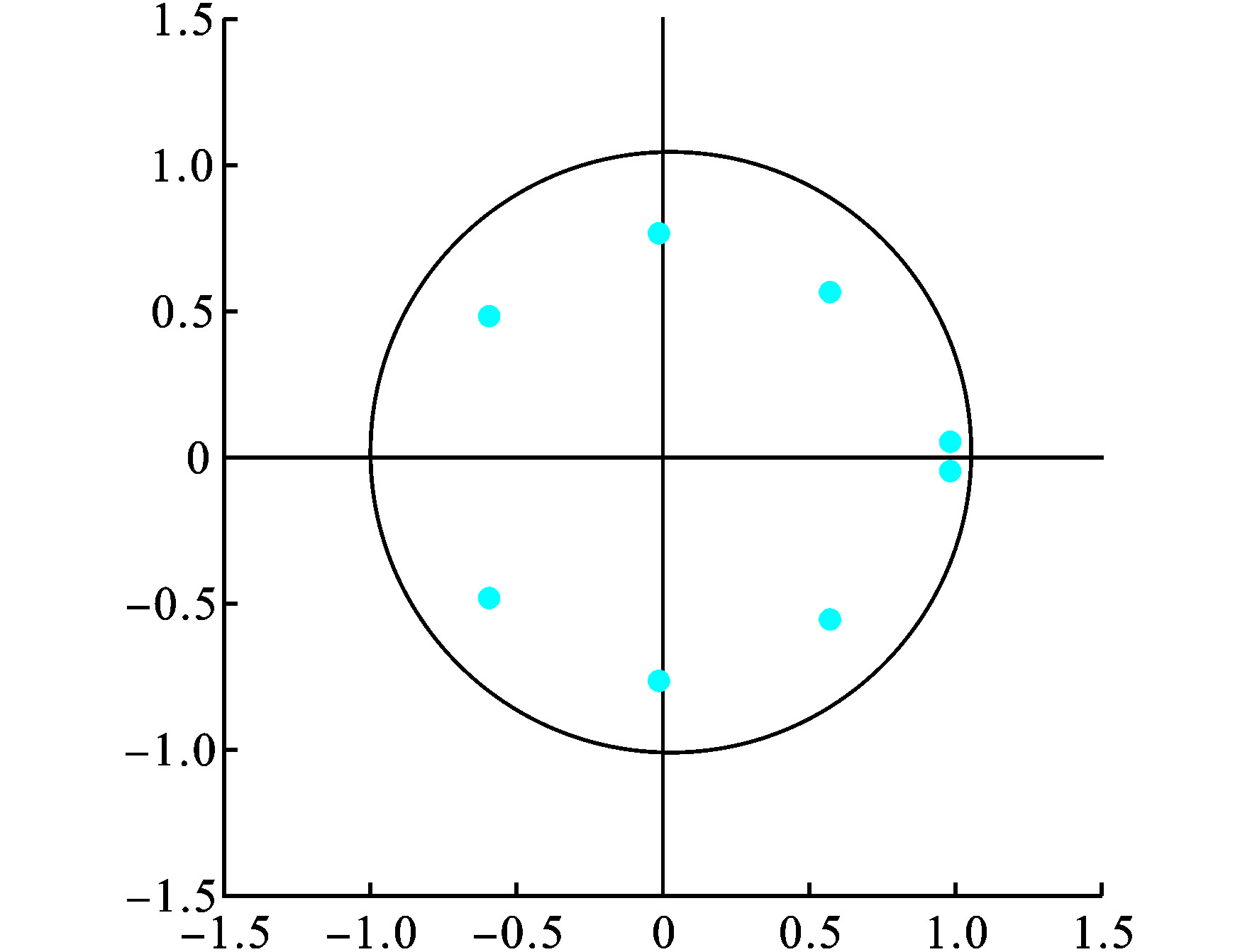
在确定了变量间的协整关系后,应用AR根方法验证协整关系的平稳性。得到AR根模的倒数见图2,8个单位根模倒数均在单位圆内,表明所得到的协整方程是稳定的。根据能耗强度、煤炭消费比例和SO.*?>=>2排放量对于CO.*?>=>2排放强度的弹性系数的含义,能耗总量每减小1%,CO.*?>=>2排放强度可以减小1.122823%;煤炭消费比例每减小1%,CO.*?>=>2排放强度可以减小0.291525%;SO.*?>=>2排放量每减小1%,CO.*?>=>2排放强度可以减小0.110033%。这表明,节能对于降碳的协同效应最为显著,其次为能耗结构优化,SO.*?>=>2减排对其也有一定的协同效应。
对Lnse、Lnei和Lncr进行协整检验,得到不同VAR滞后阶数对应的各准则数值见表4,最佳滞后阶数为2。
迹统计检验结果和最大特征根统计检验结果见表5,表明3个变量之间存在着长期协整关系。
同时得到Lnse、Lnei、Lncr和Lnse之间的协整方程为式(7)。
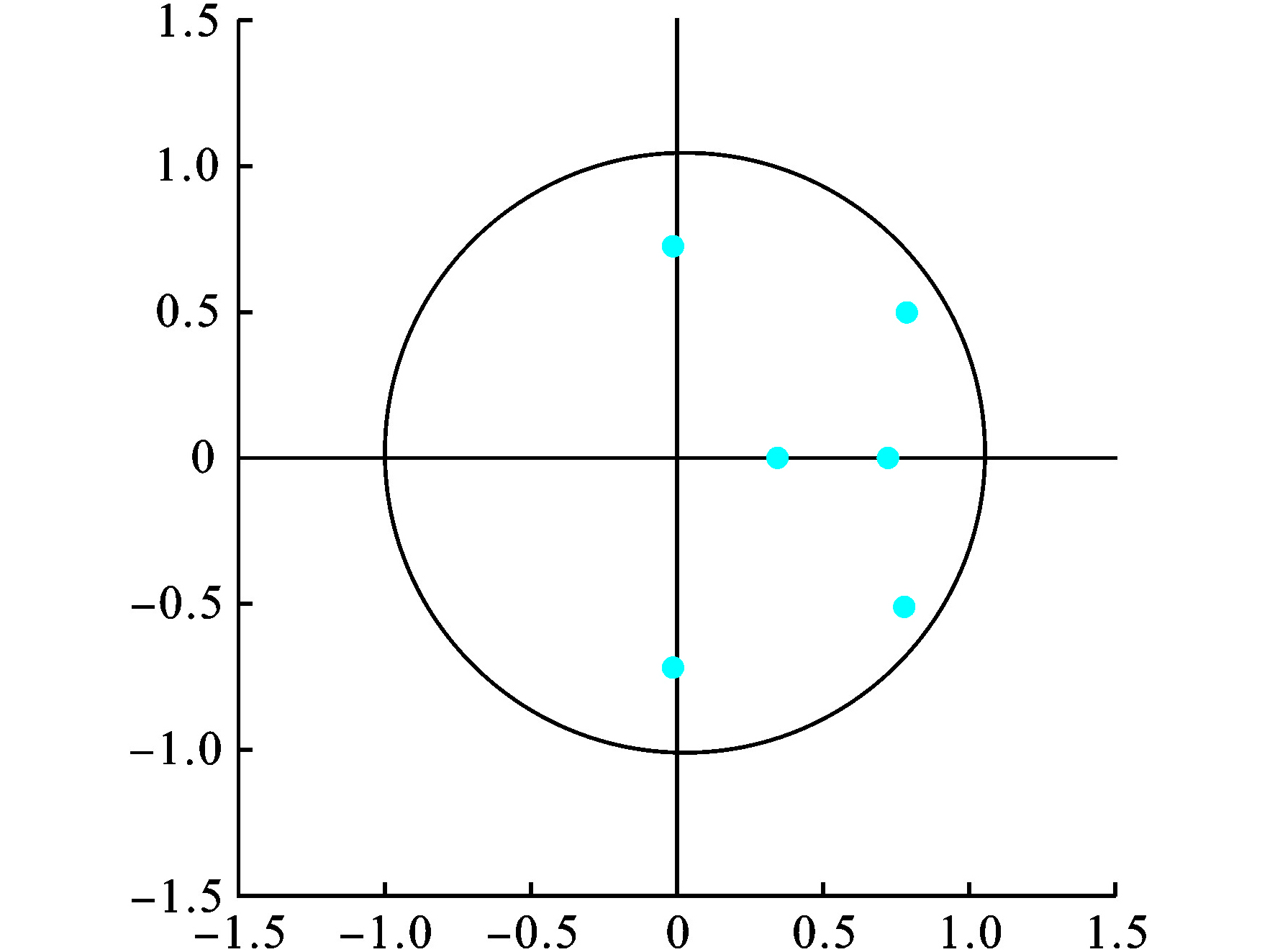
AR根模的倒数见图3。
图3可见,6个单位根模倒数均在单位圆内,协整方程稳定。根据能耗强度、煤炭消费比例对于SO.*?>=>2排放强度的弹性系数的含义,能耗总量每减小1%,SO.*?>=>2排放量可以减小0.019573%;煤炭消费比例每减小1%,SO.*?>=>2排放量可以减小2.37775%。这表明,能耗结构优化对于SO.*?>=>2减排的协同效应最为显著,节能对其也有一定的协同效应。
-
4个变量均存在协整关系,对其进行分组Granger因果检验,结果见表6。
表6可知,在5%的显著性水平下,拒绝“能耗强度波动不是CO.*?>=>2排放强度波动的Granger原因”、“CO.*?>=>2排放强度波动不是煤炭消费比例波动的Granger原因”、“SO.*?>=>2排放波动不是CO.*?>=>2排放强度波动的Granger原因”、“CO.*?>=>2排放强度波动不是SO.*?>=>2排放波动的Granger原因”、“能耗强度波动不是煤炭消费比例波动的Granger原因”、“SO.*?>=>2排放波动不是能耗强度波动的Granger原因”、“能耗强度波动不是SO.*?>=>2排放波动的Granger原因”、“煤炭消费比例波动不是SO.*?>=>2排放波动的Granger原因”,在10%的显著性水平下,拒绝“煤炭消费比例波动不是CO.*?>=>2排放强度波动的Granger原因”。这表明,能耗强度、SO.*?>=>2排放、煤炭消费比例的变动均对CO.*?>=>2排放强度变动具有明显的影响;CO.*?>=>2排放强度、能耗强度、煤炭消费比例的变动均对SO.*?>=>2排放变动具有明显的影响;SO.*?>=>2排放变动对于能耗强度变动也有明显影响;能耗强度和CO.*?>=>2排放强度的变动则对煤炭消费比例变动有着明显影响。
-
上述2个VAR(2)模型均是稳定的,可以进行脉冲响应分析和方差分解。脉冲响应函数描述的是一个内生变量对残差冲击的反应。具体而言,它描述的是在随机误差项上施加一个标准差大小的冲击(来自系统内部或外部)后对内生变量的当期值和未来值所产生的影响(动态影响)。设置脉冲响应函数的追踪期为10期,得到Lnci相对于自身、Lnei、Lncr和Lnse的响应函数曲线见图4。图4(a)~(d)中实线表示随着预测期数的增加,Lnci、Lnei、Lncr和Lnse对于Lnci一个标准差新息的脉冲响应,虚线表示相应脉冲响应图像两侧加或减两倍标准差的信息带。
图4可见,截至第5期,Lnci、Lnei和Lnse对Lnci始终具有一定的正效应,自第6期开始呈现负、正效应交替的情形;Lncr对Lnci的正效应则持续到第9期,后续开始呈现负效应。这表明,中国的降碳、节能、能耗结构优化和减排结果均对今后短期内的降碳产生一定的累积促进效应,但是长期来看并不稳定。
Lnse相对于自身、Lnei、Lncr的响应函数曲线见图5。图5(a)~(c)中实线表示随着预测期数的增加,Lnse、Lnei和Lncr对于Lnse一个标准差新息的脉冲响应,虚线表示相应脉冲响应图像两侧加或减两倍标准差的信息带。
图5可见,Lnse、Lnei和Lncr对Lnse具有显著的正效应。这表明,中国的节能、能耗结构优化以及SO.*?>=>2减排已对SO.*?>=>2减排产生了明显的累积促进效应,这在一定程度上也解释了随着中国能耗强度下降、煤炭消费比例降低,SO.*?>=>2排放总量持续下降的原因。
-
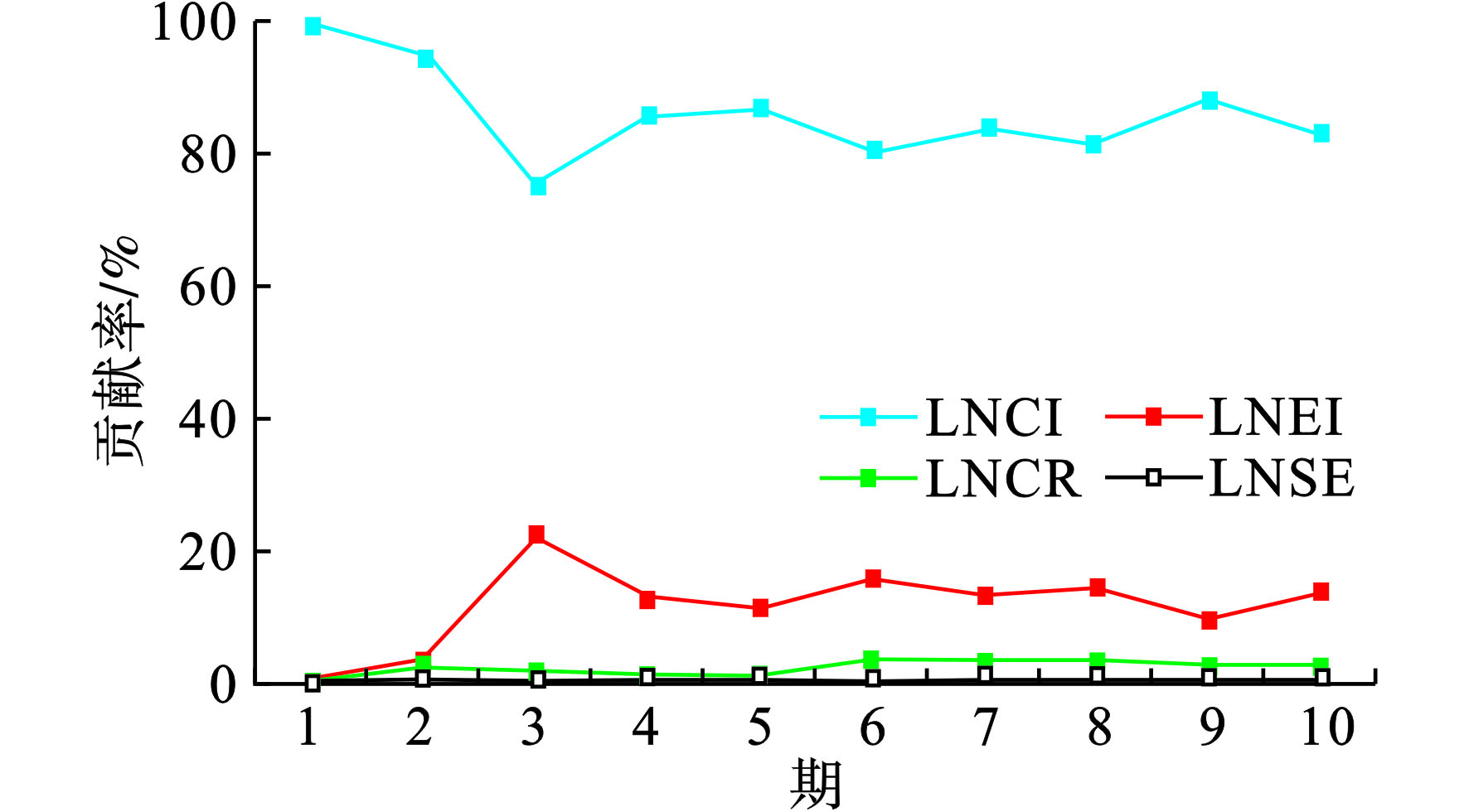
方差分解用来分析影响内生变量变化的结构冲击的贡献度,其目的是确定系统中每一个内生变量的主要影响因素,CO.*?>=>2排放强度的方差分解结果见图6,表示随着预测期数的增加,不同因素对于CO.*?>=>2排放强度变动的贡献度。
图6可知,在CO.*?>=>2排放强度的变动中,其自身的贡献最大,基本保持在80%以上,能耗强度、煤炭消费比例和SO.*?>=>2排放量的贡献率则基本稳定在8%、5%和3%以上,第10期四项因素的贡献率依次为83.15%、8.44%、5.19%和3.22%。
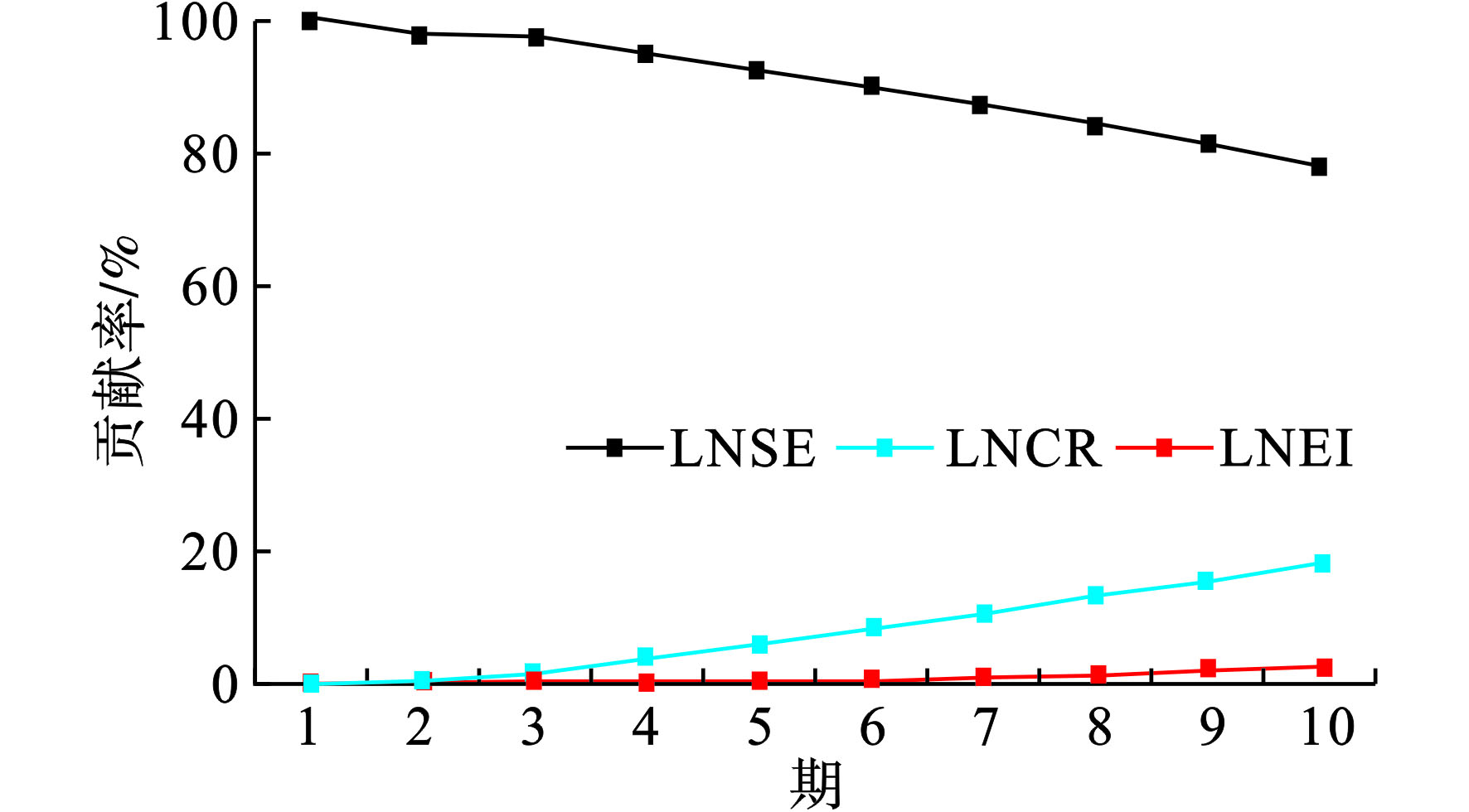
SO.*?>=>2排放量的方差分解结果见图7,表示随着预测期数的增加,不同因素对于SO.*?>=>2排放强度变动的贡献度。
图7可知,在SO.*?>=>2排放量的变动中,其自身贡献最大,但呈现下降趋势,由第1期的100%下降至第10期的78.53%,煤炭消费比例的贡献呈现明显上升趋势,第10期增至18.51%,能耗强度则增至2.96%。这表明,继续加强降碳和减排工作,有利于CO.*?>=>2排放强度与SO.*?>=>2排放量的持续下降;其次,加强能耗结构的优化,降低煤炭消费比例,同时注重节约能源,有利于实现降碳和减排的协同效果;最后,减排措施的实施在促进SO.*?>=>2减排的同时,一定程度上也有利于提高降碳效果。
2.1. 序列的平稳性检验结果
2.2. Johansen协整检验
2.3. Granger因果检验
2.4. 脉冲响应分析
2.5. 方差分解分析
-
通过Johansen协整检验、Granger因果检验、脉冲响应和方差分解等,对中国能耗、大气污染物排放总量和碳排放强度的关系进行分析。结果表明,节能对于降碳的协同效应最为显著,其次为能耗结构优化,SO.*?>=>2减排对其也有一定的协同效应;能耗结构优化对于SO.*?>=>2减排的协同效应最为显著,节能对其也有一定的协同效应。能耗强度与结构、SO.*?>=>2排放对碳排放具有明显的Granger影响;碳排放、能耗强度及结构也对SO.*?>=>2排放具有明显的Granger影响。降碳、节能、能耗结构优化和减排均对短期降碳产生一定的累积促进效应,但是长期并不稳定;节能、能耗结构优化以及SO.*?>=>2减排则对SO.*?>=>2减排具有显著的累积促进效应。碳排放强度的变动贡献中,按照贡献率高低依次为其自身、能耗强度、能耗结构和SO.*?>=>2排放量;SO.*?>=>2排放的变动驱动因素则依次为其自身、能耗结构和能耗强度。今后中国应持续降低能耗强度,科学优化能耗结构,积极开发和应用减排降碳技术,以最大化节能减排降碳效果。


 下载:
下载: