-
随着我国工业经济的迅速发展,生态环境保护与经济增长之间的关系权衡成为可持续发展面临的重要问题[1-2]。重工业的发展,使得大量工业污染物排入水环境中,造成生态环境的破坏[3-4]。在研究经济发展与水环境污染关系时,学者通过EKC来反映二者的关系,研究发现二者之间呈现“倒U型”关系[5-6]。在研究中国经济增长与环境污染脱钩关系时,学者们研究发现我国大部分省份表现为强脱钩状态,少数省份则为弱脱钩状态[7]。在研究环境污染的影响因素问题中,国内外学者采用不同的模型实证分析了各影响因素及其影响程度,IPAT及其拓展模型如STIRPAT模型的研究越来越广泛[8-13],其主要应用于碳排放、能源消耗等导致的环境问题方面,在水环境污染驱动力的研究中,有学者利用STIRPAT模型分析了水污染的影响因素及其影响程度[14-15]。但关于我国整体水环境污染影响因素的系统研究较少。
本文根据文献[16-17]研究水污染的指标选取,在STIRPAT模型的基础上加入相关变量,利用我国省市面板数据系统,分析影响水环境污染的各因素影响程度。
全文HTML
-
STIRPAT模型是IPAT模型的拓展模型,是由EHRLICH等[8,18-19]提出的,其模型的最初形式,见式(1)。
式(1)中,I为环境压力,P为人口规模,A为富裕程度,T为技术进步。
该模型认为,环境压力I是由人口规模P、富裕程度A以及技术进步T共同决定的。由于该模型在应用中的局限性性,YORK et al[20]对IPAT模型修正得到的非线性回归模型STIRPAT模型,其标准形式,见式(2)。
式(2)中,I、P、A、T代表的含义与式(1)相同,a、b、c、d分别为模型影响系数与各变量的指数,e为随机误差项。在实际应用中,为减少异方差影响,对式(2)两边作对数处理,为方便表达各系数,均用β来表示,处理后得到线性模型,见式(3)。
-
水环境污染主要是由于人口的增长、社会经济的快速发展、城镇化的加快等共同导致的。为综合研究我国水污染的各影响因素以及影响程度,本文在式(3)的基础上再加入产业结构、用水结构、城镇化等指标,故将式(3)进一步拓展得式(4),即STIRPAT模型的拓展线性回归方程式。
式(4)中,I为水环境质量,本文用废水排放总量、COD值和氨氮排放量作为衡量水污染指标;P为人口规模;A为富裕程度,用人均GDP表示;T为技术水平,用废污水排放强度表示;ur为城镇化率,以城镇人口占总人口的比重来表示;st为用水结构,以生活用水量占用水总量比例来表示;cs为产业结构,以工业产值占GDP比重来表示。
我国研究水污染情况时主要统计指标有废水排放总量、COD排放量和氨氮排放量。根据我国学者[21-22]对水污染的研究,本文将废水排放总量、COD排放量以及氨氮排放量分别作为衡量我国水环境污染的指标,与各水污染影响因素作模型检验分析,得到各水环境污染因素对水污染的影响程度。水环境污染评价指标体系,见表1。
本文选取我国31个省(自治区、直辖市)面板数据作为研究对象。数据来源于2009~2018年《中国统计年鉴》《中国环境统计年鉴》以及各省市、自治区统计年鉴。
1.1. STIRPAT模型
1.2. 数据选择与来源
-
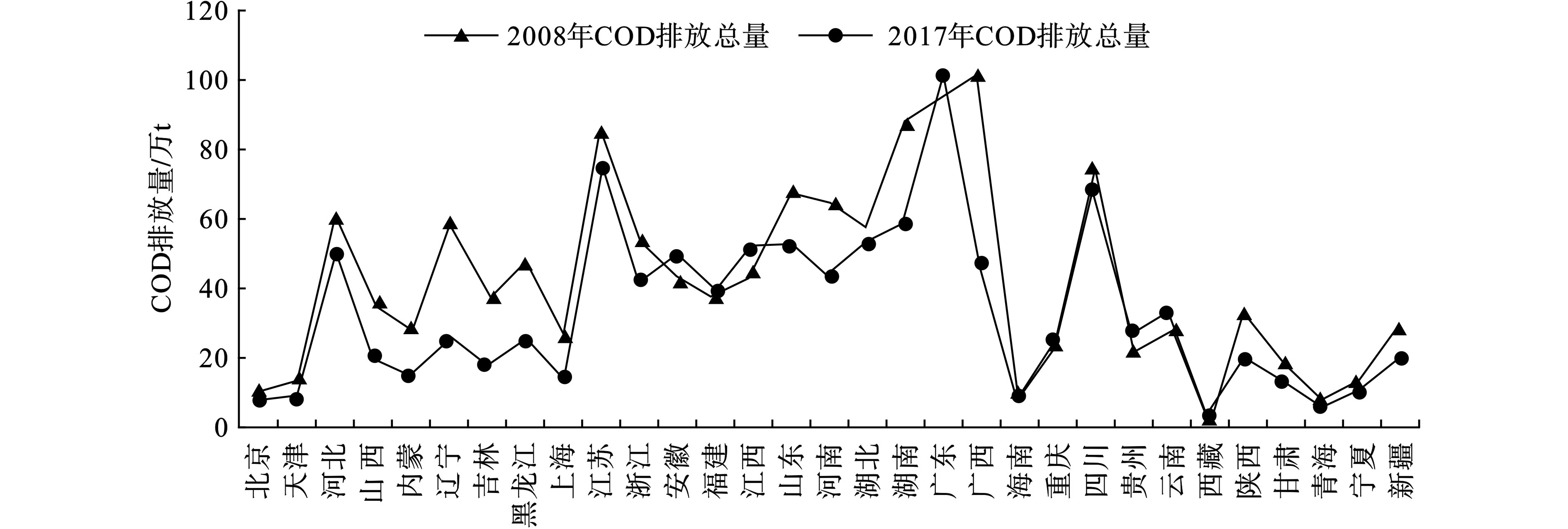
本文选取2008~2017年10年的省际面板数据作为研究对象。为了更好地比较10年间的变化,本部分选取2008和2017年的数据进行对比,31个省(自治区、直辖市)废水排放总量、COD排放量、氨氮排放量,见图1~3。
图1可知,除个别省份外,其他省市废水排放量在2017年均增长,且各地区增长幅度不同。
图2可知,除个别省份外,省市COD排放量在2017年均下降。
图3可知,2008和2017年各省市氨氮排放量未呈现规律性变化。
以废水排放量表示水污染,在一定程度上认为我国水污染情况严重了 ;以COD排放量表示水污染,在一定程度上认为我国水污染情况减轻了;以氨氮排放量表示水污染,不能从数量上确定我国水污染情况。因此,以废水、COD、氨氮排放量的数量变化无法确定我国水污染总体情况,故本文通过废水排放量、COD排放量和氨氮排放量这3项指标分别作为模型(4)的因变量,分析不同指标下我国水环境污染因素影响程度。
-
根据STIRPAT模型的拓展模型(4),做自变量与各因变量之间的回归分析,选取我国31个省(自治区、直辖市)的面板数据作为研究对象,在回归分析之前,为确保面板数据的平稳性,避免出现伪回归,对各变量进行单位根检验。本文选择了LLC检验,即相同单位根检验,假设“存在单位根”,检验结果,见表2。
除用水结构st与产业结构cs这两个变量不能拒绝原假设,检验结果是不平稳的,其他变量均能拒绝原假设,检验结果为平稳。变量拒绝原假设,即不存在单位根,变量表现为平稳,没有随机趋势或确定趋势,在后面进行回归分析时将避免伪回归现象。变量不能拒绝原假设,即存在单位根,变量表现为不平稳,在回归分析中可能存在伪回归现象。因此将用水结构st与产业结构cs这两个变量进行一阶差分后进行单位根检验,检验结果均能拒绝原假设,表现为平稳。因此,各变量均通过平稳性检验。
-
根据模型(4),对各变量进行了平稳性检验,且各变量均通过平稳性检验,故利用stata16.0对模型进行OLS回归参数估计。分别以废水排放量、COD排放量和氨氮排放量为因变量进行OLS回归,见表3~5。
表3可知,当废水排放总量为因变量时的回归结果,用水结构st与产业结构cs未通过t检验,各项指标系数均为正值,与因变量之间呈现正相关,但各系数均较小,不能够密切反映出与因变量之间的数量关系。
表4可知,当COD排放量为因变量时的回归结果,各参数均通过t检验,对各自变量进行VIF(方差膨胀因子)多重共线性检验,结果各变量VIF值均小于10,通过检验,不存在多重共线性。
由回归结果可知各变量之间的关系,见式(5)。由F检验值,调整后的R2值可知,模型的整体拟合效果较好,式(5)能够较好的反映各变量之间的关系;
表5可知,当氨氮排放量为因变量时的回归结果,各参数均通过t检验,调整后的R2值较表4稍小,且各指标的系数均较小,不能够密切反映出与因变量之间的数量关系。根据以废水排放量、COD排放量和氨氮排放量为水污染衡量指标,分别作模型(4)的回归分析可知,COD排放量较废水与氨氮的排放量更能反映与各水污染因素之间的关系。
-
由OLS回归方程可知,影响我国水污染指标COD值的因素中,人口规模、人均GDP、排放强度、产业结构的参数均为正值,说明这些变量与COD之间呈正相关关系,即这些变量的增加会使COD增长;城市化水平和用水结构的参数为负值,与COD之间呈负相关,即城市化水平和用水结构会抑制COD的增长。
(1)与COD呈正相关的变量中:1)人口规模每增加1%,COD排放量增加0.86%。人口的增加会造成用水量的增加,相应随着人们生活水平的提高,对水的需求量增大,废水排放也相应的增加;2)人均GDP每增加1%,COD排放量增加0.63%,说明人均GDP的增加对COD值的影响也较大。按人均GDP衡量经济发展水平,我国是中等收入国家,根据环境库兹尼茨“倒U型”曲线,我国还处在“倒U型”曲线的左边,水环境压力会随着人均GDP的增加而增加;3)排放强度每增加1%,COD值增加0.535%。排放强度是根据废污水排放总量占GDP的比例来计算的,排放强度越高,则说明废水排放量的增加速度快于GDP增长速度;4)产业结构每增加1%,COD值增加0.48%。产业结构是工业产值占GDP的比例,工业产值占GDP的比例越高,对环境造成的压力越大。在以上与COD呈正相关的变量中,人口规模是影响最为显著的因素。
(2)与COD呈负相关的变量中:1)城市化水平每增加1%,COD值减少0.53%。城市化水平用城市人口占总人口的比重来表示,这说明导致水环境污染的原因是人口规模,并不是城市人口占总人口的比重越大水污染就越严重;2)用水结构每增加1%,COD值减少0.32%。用水结构是生活用水占总用水量的比例,说明造成水污染的因素中,工业用水造成的污染更大。
2.1. 2008和2017年我国水污染情况
2.2. 平稳性检验
2.3. 回归分析
2.4. 结果分析
-
本文通过对2008~2017年我国相关面板数据分析水环境污染因素得到以下结论。
(1)较2008年废水排放总量,我国31个省(自治区、直辖市)2017年废水排放总量基本都呈现上升趋势;COD排放量除个别省份外,均呈现下降趋势;氨氮排放量除个别省市外,均呈现上升趋势。
(2)在影响水污染的因素不变时,与废水排放总量与氨氮排总放量相比,COD排放量作为水环境污染的衡量指标更合适,能够反映出水环境污染因素及其影响程度。
(3)在影响水环境污染的各因素中,人口规模是造成水污染的最重要因素,其次,人均GDP、工业发展对水污染的影响也较大。这些因素的增长会相应增加水环境污染程度。废水中COD的含量越高,水环境污染程度越高,废水来源于工业废水和生活废水,本研究发现造成水污染的废水排放中,工业废水对水污染的影响较大。



 下载:
下载: