-
研究水源地高精度水质预测模型,可提高对出水环境中水质污染的预测准确性,从而有助于及时发现当地水质问题,它的准确性和可靠性会直接影响水环境管理的科学决策。溶解氧 (dissolved oxygen,DO) 指在水中可溶解的氧气分子,其溶度直接影响着水中生物的呼吸和代谢过程。因此,对DO的预测是水质预测中的一个重要组成部分。
近年来,随着人工智能技术的发展,数据驱动模型在水利和环境保护领域的模拟中得到了广泛应用。除开使用GIS构建水质模型,还有三类方法可用于水质预测。第一类方法是以逐步回归为代表的传统预测方法,例如支持向量机[1] (support vector regression,SVR) ,在解释性和小数据集上具有优势。第二类是以机器学习为代表的预测方法,如BP[2] (back propagation) 神经网络、长短期记忆神经网络[3-5] (long short-term memory networks,LSTM) 、门控循环单元[6-9] (gated recurrent unit,GRU) ,此类方法提高了对非线性问题的处理能力,但是超参数的合理选取制约了其预测精度的提升。目前普遍采用群体智能算法进行寻优,如粒子群优化算法[10-11] (particle swarm optimization,PSO) 、灰狼优化算法[12] (grey wolf optimizer,GWO) 、鲸鱼优化算法[13-15] (whale optimization algorithm,WOA) 。第三类是组合预测法,组合方式分为两种,第一种是基于两个或两个以上预测器的组合方式,如GNN (graph neural network) -LSTM模型[16]、CNN (convolutional neural networks) -GRU模型[17]、TimeGAN (time-series generative adversarial network) -CNN-LSTM模型[18]等,该方式的特点是利用各个模型的优势来克服单一预测模型的不足,但预测结果往往存在较大的不确定性;另一种组合方式是基于信号分解技术的预测方法,该方法利用信号分解技术将原始时序数据分解成若干更具规律的子序列分量,通过对子序列分量进行预测,重构得到最终的预测结果,如小波降噪-长短时记忆网络 (DWT-LSTM) 模型[19]、主成分分析和长短时记忆网络 (PCA-LSTM) 模型[20]、变分模态分解-改进猫群优化算法-门控循环单元 (VMD-ISCO-GRU) 模型[21]。
基于上述分析,本研究针对水质时序数据非线性强、随机波动性大导致的模型预测精度不高的问题,按照“数据处理-模型预测-参数寻优”的思路,对数据采用差分的方式进行处理,降低原始水质数据的部分波动性;利用GRU模型处理时间序列的优势实现对溶解氧的预测,在模型输出时通过CNN模型获取局部特征,提高模型的精准度;由于GRU超参数对网络模型预测性能具有较大影响,使用群体智能算法中的鲸鱼优化算法进行寻优;为解决鲸鱼优化算法中初始化种群质量较低、早熟收敛、受参数设置敏感等问题,引入混沌映射机制、自适应惯性权重、遗传算法 (genetic algorithm,GA) 进行改善。最后基于长江干流的调关水质监测断面所采集数据为研究对象,实验结果表明,本研究模型可以有效提高调关溶解氧预测精度,为调关水质监测管理和维护提供科学决策的依据。
-
WOA是一种启发式优化算法,通过模拟座头鲸的搜索策略和围捕机制来寻找问题的最优解。其中有三个重要阶段:收缩包围、螺旋上升和随机搜索。这些阶段的协同作用使得鲸鱼优化算法成为一种有效的优化算法,可应用于各种需求最优解的问题。
1) 收缩包围。WOA算法的搜索范围是整个解空间,需要先确定猎物的位置以便包围。由于最优解在算法中不是先验已知的,WOA算法假定当前的最佳候选解是目标猎物。在确定了猎物以后,其它鲸鱼会尝试向猎物更新自己的位置,这一行为的数学模型如公式(1)所示。
式中:
$ P\left(t\right) $ 代表当前鲸鱼所在的位置;$ {P}_{\mathrm{b}\mathrm{e}\mathrm{s}\mathrm{t}}\left(t\right) $ 代表猎物所在位置,$ t $ 是当前迭代的次数;$ A $ 和$ B $ 分别是系数向量;$ a $ 代表线性权重,随着迭代次数的增加,$ a $ 从初始值2线性递减至0;$ {r}_{1} $ 和$ {r}_{2} $ 分别为区间[0,1]之间的随机向量。2) 螺旋上升。在觅食过程中,收缩包围和螺旋上升两种机制是同时进行的。在优化过程中,当系数向量
$ \left|A\right| \lt 1 $ 时,鲸鱼群会等概率的选择收缩包围或螺旋上升,如公式(4)所示。式中:
$ b $ 为常数;$ l $ 为区间[−1,1]之间的随机数;$ p $ 为区间[0,1]之间的随机数。3) 随机搜索。除开收缩包围和螺旋更新两种位置更新机制外,鲸鱼还可以随机游动搜索猎物。当系数向量
$ \left|A\right|\ge 1 $ 时,鲸鱼会根据整个群体的位置随机搜索猎物,如公式(5)所示。式中:
$ {P}_{\mathrm{r}\mathrm{a}\mathrm{n}\mathrm{d}}\left(t\right) $ 为在种群中随机选择的鲸鱼个体。 -
1) 引入混沌映射机制。MOHAMMED等[14]研究表明WOA算法的初始种群质量会影响算法的搜索效率和全局最优解的探索能力。标准的WOA算法使用随机算法生成种群,无法保证种群在整个解空间的完全均匀分布,对算法的全局寻优能力会造成一定的影响。因此,将Tent混沌映射机制引入到WOA算法中,将原始随机生成的种群更改为离散映射,提高初始种群质量。Tent混沌映射的数学模型如公式(6)所示。
式中:
$ X\left(n\right) $ 为当前迭代的个体值;$ X(n+1) $ 为下一次迭代的个体值;$ a $ 为控制参数,取值范围在[0,2]之间。2) 引入自适应惯性权重。标准WOA算法中的权重为线性权重,
$ a $ 会随着迭代次数的增加从2线性递减到0,一定程度上造成搜索猎物不彻底,包围猎物速度慢的问题。因此,提出一种非线性的收敛方式,克服线性收敛对算法带来的不利影响。自适应惯性权重的数学模型如公式(7)所示。式中:
$ t $ 表示当前迭代的次数,$ n $ 表示最大迭代次数,$ rand $ 表示在区间[0.5,1]之间的一个随机数。3) 引入遗传算法。遗传算法通过使用进化 (如选择、交叉和变异) 的操作来逐步改进解的质量,从而找到问题的最优解和接近最优解。下面对遗传算法的步骤进行介绍。
选择:采用锦标赛选择法,即随机从种群中选择部分个体,并从中选择最优的个体作为父代,直到父代数量达到设定的数量。
交叉:种群中的个体在经过选择后,并进行配对,以概率
$ {P}_{i} $ 进行均匀算术交叉。使用随机数与交叉概率$ {P}_{i} $ 进行对比,较大,返回父代;否则,对父代进行交叉运算,形成两个新的子代。交叉操作的数学模型如公式(8)所示。式中:
$ {X}_{n+1}^{i} $ 和$ {X}_{n+1}^{j} $ 表示由父代产生的子代;$ {X}_{n}^{j} $ 和$ {X}_{n}^{i} $ 表示两个相配对的父代;$ rand $ 表示在区间[0,1]之间的随机数。变异:对于经过交叉操作之后产生的子代,以概率
$ {P}_{m} $ 进行变异操作,其数学模型如公式(9)所示。式中:
$ {Y}_{n+1} $ 表示变异产生的子代;$ {X}_{n} $ 表示当前个体;$ F\left({X}_{n}\right) $ 表示该个体的适应度;$ {P}_{rand} $ 表示一个在区间[0,1]之间的随机实数;$ u $ 表示[$ {x}^{u} $ ,$ {x}^{l} $ ]之间的一个满足均匀分布的随机数,$ {x}^{u} $ 表示个体所在区间的下界,$ {x}^{l} $ 表示个体所在区间的上界。 -
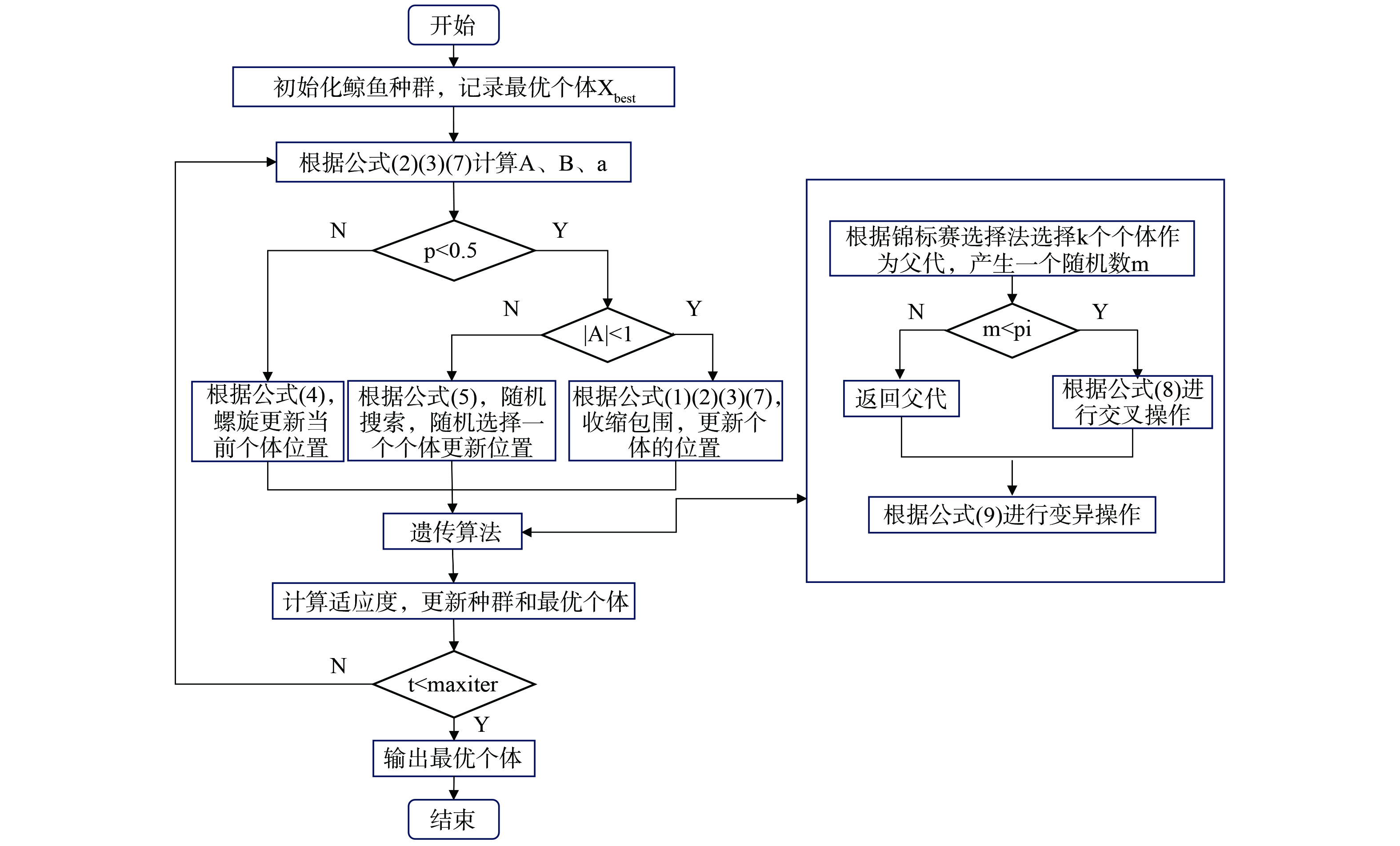
IWOA算法的具体步骤如图1所示。
-
GRU是一种基于 LSTM 网络的变体,它在很大程度上减少了传统循环神经网络 (recurrent neural network,RNN) 中的梯度爆炸或消失带来的部分影响。对比LSTM,GRU使用“更新门”替代了LSTM中的遗忘门和输出门,优化了网络结构,提升了前向传播的速度。
-
CNN的核心思想是利用卷积层和池化层对输入数据进行特征提取和下采样,然后通过全连接层进行分类或回归。水质数据为一维数据,采用一维卷积神经网络捕获隐藏信息,实现数据的特征提取。假设水质数据的输入大小为4×1,和同样大小的卷积核进行卷积操作,并沿着时间轴按步长为1进行滑动计算,就能提取水质数据的短期特征。
-
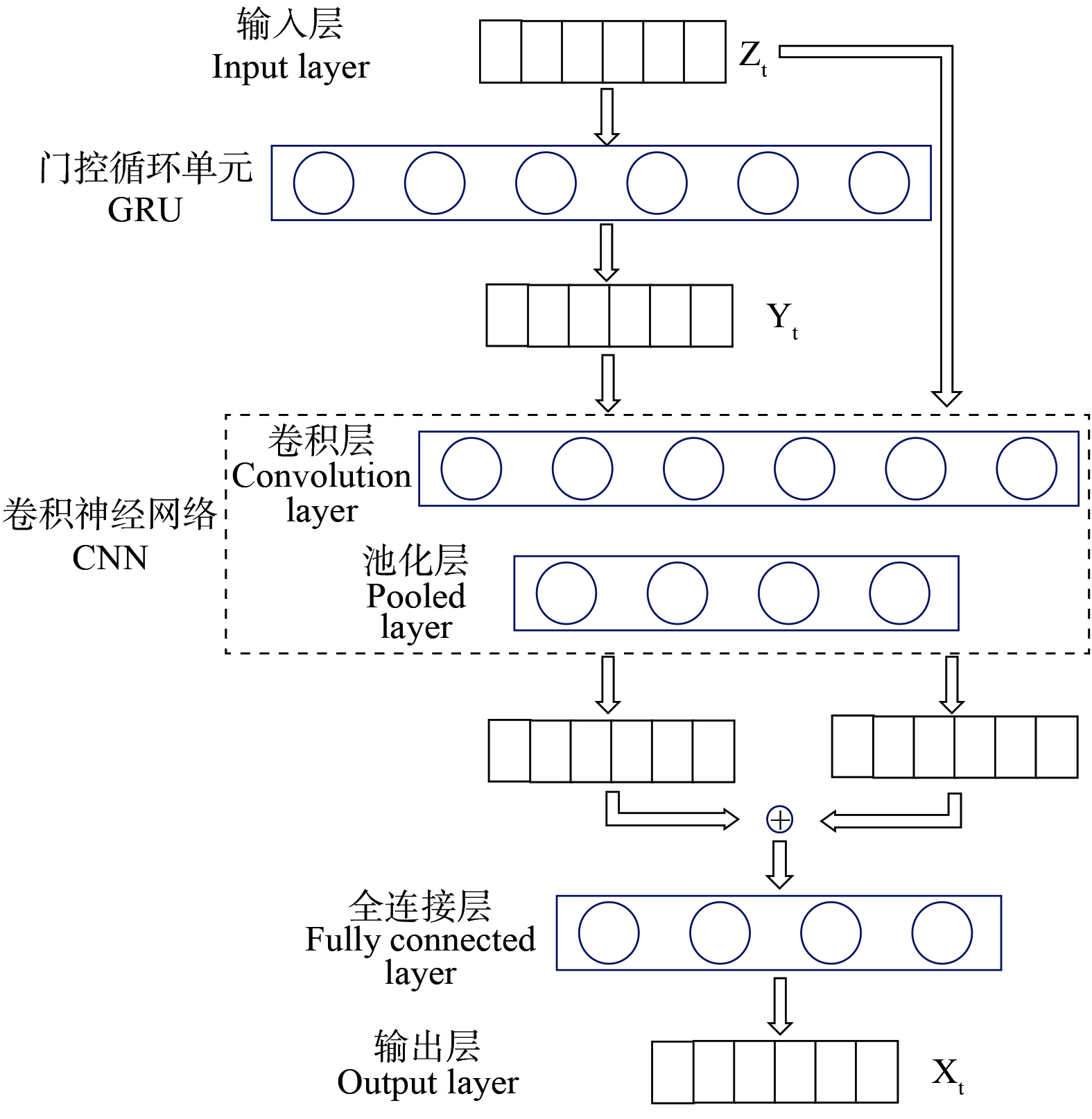
GRUC+混合模型如图2所示,由输入层、GRU网络、CNN网络、全连接层和输出层5个部分构成,其中CNN网络包含卷积层和池化层。在该模型中,将采集到的数据经过缺失值和异常值处理之后并进行归一化,就能够得到输入层的数据Zt。Zt使用pyTorch框架的DateLoader进行数据批次的划分,输入到GRU层提取时间特征后得到特征向量Yt。此时将Yt和Zt同时通过卷积层和池化层,分别对输入数据和输出数据进行局部感知操作,捕捉数据中的细节特征。将CNN网络输出的两个特征向量进行拼接,经过全连接层的处理后,得到预测数据,进而预测DO含量。
-
为了评估模型预测DO的性能和效果,选用4种不同的评价指标,分别是平均绝对百分比误差 (mean absolute percentage error,MAPE) 、均方根误差 (root mean square error,RMSE) 、平均绝对误差 (mean absolute error,MAE) 和决定系数R2。
-
选用4个测试函数对混合策略的IWOA算法进行性能的评估,同时进行消融实验以及对比实验。测试函数相关信息如表1所示。
保证测试的有效性,设置各算法的运行环境相同,即种群规模为50,最大迭代次数为600,个体维度为30。并且为保证实验可信度和数据准确性,将算法运行40次,并计算平均值,各算法对测试函数优化求解的结果如表2所示。
由表2可知,基于混合策略的IWOA在4个测试函数的实验中,寻优能力相比其它算法效果最好,平均值以及最优值均一致收敛到全局最优解。Tent混沌映射提高了马尔可夫过程的随机性,即扩大了种群的分布范围,使其可以处理更加复杂的搜索空间;自适应惯性权重的在4个测试函数中效果较为出色,其可以在搜索过程中平衡全局搜索和局部搜索的权重,克服线性权重带来的影响;遗传算法对于所有函数都具有性能提升,在Griewak函数达到了最优,其为WOA算法提供了更广泛的搜索空间,提升了算法的寻优能力。在Sphere和Ackley这两个函数的测试结果中,IWOA的标准差最优,说明其具有更好的稳定性和一致性;IWOA的最优解较为接近理论最优解,表明该算法相较于其它算法,收敛精度更高。在Griewank和Rastrigin函数中,WOA相关算法均能稳定搜索到最优解,说明WOA的相关算法对这两个函数适应度较高;GWO算法虽能够找到全局最优解,但是相较于WOA相关算法的标准差更高,说明IWOA算法的鲁棒性更高。为了更好的体现IWOA的性能,10种算法在Griewank和Rastrigin函数的收敛曲线如图3所示,与对比算法相比,基于混合策略的IWOA具有更高的寻优精度和更快的收敛速度。
-
1) 实验数据及预处理。本研究实验数据来自于长江干流的调关断面所采集数据,2019年1月1日—2021年12月31日共5 000多条数据,其中包含温度、PH、DO含量、电导率、浊度、高锰酸钾指数、氨氮含量、总磷含量、总氮含量。对于采集到的数据不能够直接使用,为保证数据的真实性,其存在的部分异常值和缺失值需要经过处理。
对于缺失数据采用线性插值法进行处理。采用前一天的当前缺失时刻的数据,并对前后共5条数据取平均值进行填充。
异常数据是在一段时间范围内偏离大部分数据的值。本研究采用
$ 3\sigma $ 原则处理异常数据,当数据与平均值的绝对值差值大于3倍的标准差,将该数据移除并使用线性插值法进行填充。原始数据中的各种数据由于量纲不同,产生的巨大差异可能造成模型预测能力下降、收敛速度降低和忽略小量纲数据。因此,对数据进行归一化处理是非常必要的。
将归一化之后的数据按照时序进行数据集划分,将前70%的数据划分为训练集,中间20%划分为验证集,后10%划分为训练集。
2) 对比实验及分析。为了验证IWOA-GRUC+混合预测模型的准确性,选取LSTM、GRU、GRU-CNN、GRUC+预测模型作为对比模型。将IWOA-GRUC+模型性能与对比模型进行比较,需要设置相同的模型参数,以GRU模型举例,设置输入大小为10、隐藏层神经元大小为32、层数为1层、数据批大小为32、模型学习率为0.01×10−10、优化器Adam的权重衰减即L2正则化为0.01×10−100、训练轮数为250轮。
经过前期的模型训练可知,隐藏层神经元大小、模型层数、数据批大小和学习率这些参数对模型的影响较大。因此使用IWOA模型对这4个参数进行寻优,需要设置种群的维度为4维,由前期的模型训练经验可设置种群的边界为[隐藏层神经元大小,模型层数,数据批大小,学习率],即下边界为[16,1,10,0.01×10−100],上边界为[64,3,256,0.01×10−10]。
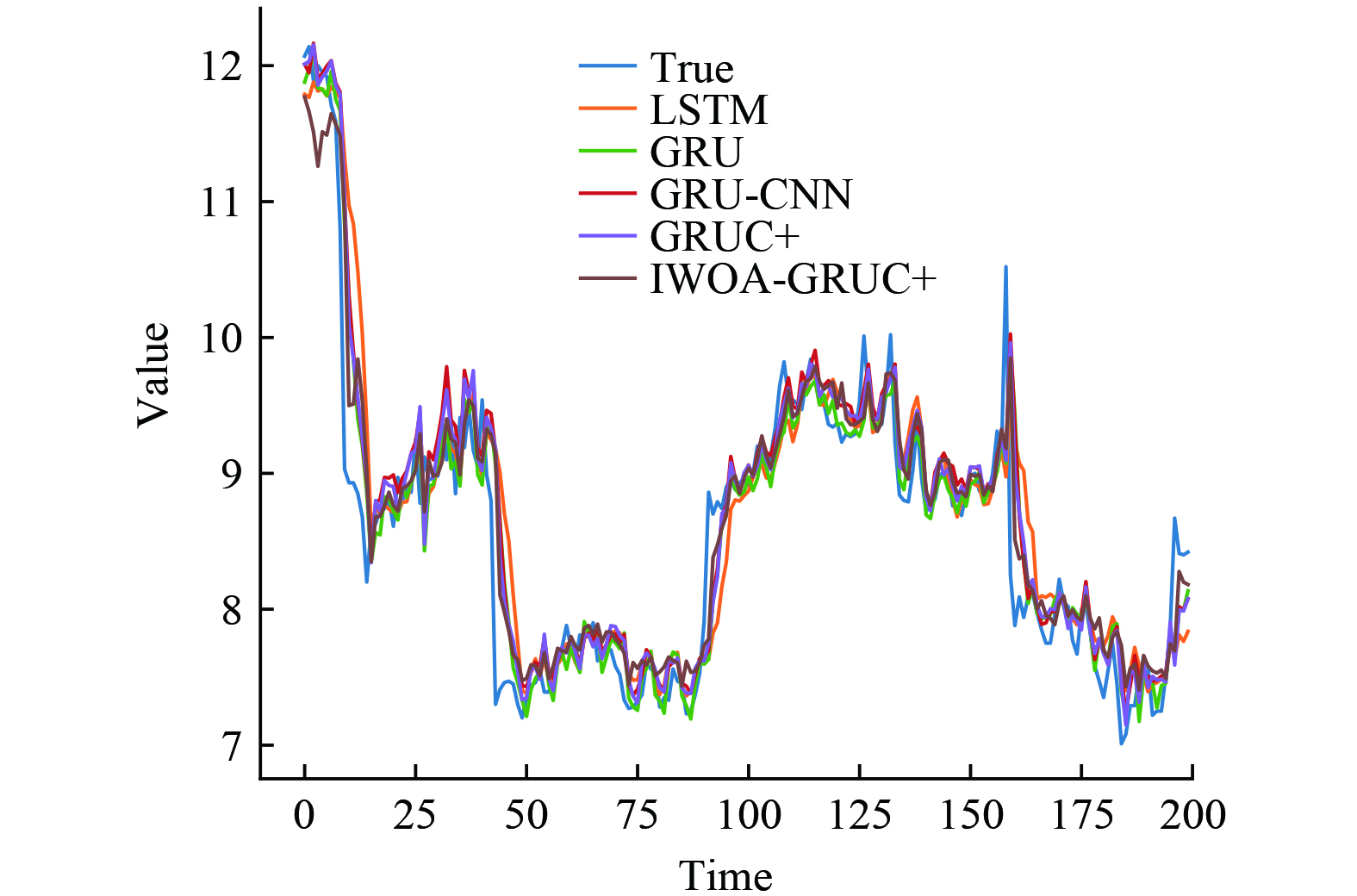
在确定相关参数之后,所提模型和对比模型的预测结果见图4,各模型的预测误差和拟合效果见表3。
从表3和图4的预测误差和预测效果来看,所提出的IWOA-GRUC+模型在该数据集上取得的预测效果最好,预测误差最小,拟合程度最高。相较于单独的GRU模型,GRU-CNN模型在MAPE和MAE指标上实现了轻微的提升,但在RMSE和R2方面却出现了一定程度的降低,表明对GRU模型的输出进行卷积处理能在一定程度上提升模型的表现。GRUC+模型对比GRU-CNN和GRU模型,预测误差均有降低,拟合程度有一定的提高,说明将输入数据与GRU的输出一起进行卷积并输出能够提升模型的预测准确率。使用改进后的IWOA对GRUC+模型进行参数寻优,可以明显看到MAPE降低了0.517%,RMSE降低了0.063,MAE降低了0.051,R2提升了3.5%。使用IWOA算法能有效的改善模型的求解性能,一定程度上提高了溶解氧预测的精度。
-
为了获得更高的DO预测精度,本研究在GRU模型的基础上,对模型的预测输出和输入数据同时进行卷积,并进行拼接,得到预测输出。确定模型之后,使用引入Tent混沌映射、自适应惯性权重和遗传算法的WOA算法对GRUC+模型进行优化。实验表明,所提出的IWOA-GRUC+模型在长期的DO预测中精度更高,拟合更优。
基于改进鲸鱼算法优化GRU-CNN的溶解氧预测
Dissolved oxygen prediction based on GRU-CNN optimized with improved whale optimization algorithm
-
摘要: 为了提高相关模型在长江调关水质断面的溶解氧预测精度,基于门控循环单元 (gated recurrent unit,GRU) ,卷积神经网络 (convolutional neural networks,CNN) 和鲸鱼优化算法 (whale optimization algorithm,WOA) 提出了一种混合预测方法。模型通过GRU提取水质数据的长期历史特征,通过CNN对GRU的输出和输入进行卷积提取短期特征,将两者进行算术拼接得到最终预测结果。通过将Tent混沌映射、自适应惯性权重和遗传算法 (genetic algorithm,GA) 引入WOA算法,解决WOA算法初始化种群质量较低,易早熟和对参数设置敏感的问题之后,再使用改进鲸鱼算法 (IWOA) 对模型进行参数寻优。实验结果表明,所提出的改进鲸鱼算法优化GRU-CNN (IWOA-GRUC+) 模型具有出色的效果,其MAPE仅为 2.27%,在RMSE、MAE和R2这几项指标上,分别达到了0.339%、0.216%和0.913%的优良表现。IWOA-GRUC+模型一定程度上提高了传统模型在溶解氧 (DO) 预测中的性能。Abstract: In order to enhance the predictive accuracy of dissolved oxygen in the Yangtze River's water quality profile, a hybrid prediction method incorporating the Gated Recurrent Unit (GRU), Convolutional Neural Networks (CNN), and the Whale Optimization Algorithm (WOA) has been proposed. The model utilizes the GRU to capture long-term historical features of the water quality data, while employing the CNN to extract short-term features from the GRU's input and output through convolutional layers. The final prediction results are obtained by concatenating the outputs of both models using arithmetic operations. To address the issues of low population quality, premature convergence, and sensitivity to parameter settings in the initialization stage of the WOA algorithm, the Tent chaotic map, adaptive inertia weight, and Genetic Algorithm (GA) are introduced into the WOA algorithm. Subsequently, the Improved Whale Optimization Algorithm (IWOA) is applied to optimize the model's parameters. The experimental results demonstrate that the proposed Improved Whale Optimization Algorithm optimized GRU-CNN (IWOA-GRUC+) model delivers outstanding performance. It achieves a notably low MAPE of 2.27% and exhibits excellent results with RMSE, MAE, and R² values of 0.339, 0.216, and 0.913%, respectively. The IWOA-GRUC+model significantly enhances the performance of traditional models in predicting dissolved oxygen (DO) levels.
-
-
表 1 标准测试函数
Table 1. Standard test functions
函数名 变量范围 最小值 Sphere [−100,100] 0 Ackley [−32,32] 0 Griewank [−600,600] 0 Rastrigin [−5.12,5.12] 0 表 2 各优化算法对测试函数的实验结果
Table 2. Experimental results of various optimization algorithms on test functions
函数名 算法 标准差 最优值 最差值 平均值 Sphere WOA 4.86×10−30 1.36×10−35 2.79×10−29 1.42×10−30 WOA_Tent 3.85×10-28 4.63×10−27 2.46×10−27 6.35×10−29 WOA_a 0 0 0 0 WOA_GA 7.29×10−30 8.69×10−37 4.67×10−29 1.24×10−30 WOA_Tent_ a 0 0 0 0 WOA_Tent_GA 9.70×10−31 1.29×10−36 6.21×10−30 2.15×10−31 WOA_a_GA 0 0 0 0 PSO 93.08 30.22 423.92 167.68 GWO 5.54×10−40 2.68×10−42 3.42×10−39 2.17×10−40 IWOA 0 0 0 0 Ackley WOA 8.06×10−15 7.54×10−15 3.95×10−14 1.56×10−14 WOA_Tent 6.93×10−15 7.54×10−15 3.24×10−14 1.86×10−14 WOA_a 0 4.44×10−16 4.44×10−16 4.44×10−16 WOA_GA 4.83×10−15 7.54×10−15 2.17×10−14 1.20×10−14 WOA_Tent_ a 0 4.44×10−16 4.44×10−16 4.44×10−16 WOA_Tent_GA 5.26×10−15 7.54×10−15 2.88×10−14 1.17×10−14 WOA_a_GA 0 4.44×10−16 4.44×10−16 4.44×10−16 PSO 4.86 2.81 19.96 6.40 GWO 2.99×10−15 2.17×10−14 3.24×10−14 2.81×10−14 IWOA 0 4.44×10-16 4.44×10-16 4.44×10-16 Griewank WOA 0 0 0 0 WOA_Tent 0 0 0 0 WOA_a 0 0 0 0 WOA_GA 0 0 0 0 WOA_Tent_ a 0 0 0 0 WOA_Tent_GA 8.66×10−17 0 5.55×10−16 1.38×10−17 WOA_a_GA 0 0 0 0 PSO 1 1.44 5.54 2.82 GWO 8.00×10−3 0 0.03 5.00×10−3 IWOA 0 0 0 0 Rastrigin WOA 0 0 0 0 WOA_Tent 0 0 0 0 WOA_a 0 0 0 0 WOA_GA 0 0 0 0 WOA_Tent_ a 0 0 0 0 WOA_Tent_GA 0 0 0 0 WOA_a_GA 0 0 0 0 PSO 24.66 61.7 180.96 127.92 GWO 1.30 5.68×10−14 6.27 0.38 IWOA 0 0 0 0 表 3 各模型的预测误差
Table 3. Prediction error of each model
模型 MAPE/% RMSE MAE R2/% LSTM 2.825 0.423 0.269 0.865 GRU 2.787 0.402 0.267 0.878 GRU-CNN 2.826 0.401 0.273 0.879 GRUC+ 2.721 0.388 0.261 0.886 IWOA-GRUC+ 2.270 0.339 0.216 0.913 -
[1] 薛同来, 赵冬晖, 韩菲. 基于GA优化的SVR水质预测模型研究[J]. 环境工程, 2020, 38(03): 123-127. [2] 张学坤. 基于SOA-SVM和SA-BP模型的溶解氧预测[J]. 人民珠江, 2021, 42(04): 99-104. doi: 10.3969/j.issn.1001-9235.2021.04.015 [3] 周泉, 胡轩铭, 王东昆, 等. 基于注意力机制优化的LSTM河流溶解氧预测模型研究[J]. 环境科学研究, 2023, 36(06): 1135-1146. [4] 方国华, 张钰, 袁婷等. 基于灰色关联-长短时记忆网络的水质预测研究[J/OL]. 安全与环境学报, 2023, 1-12. [5] YU M, NUY D, WANG K, et al. Short-term photovoltaic power point-interval forecasting based on double-layer decomposition and WOA-BiLSTM-Attention and considering weather classification[J]. Energy, 2023, 275: 127348. doi: 10.1016/j.energy.2023.127348 [6] CHI D, HUANG Q, LIU L. Dissolved oxygen concentration prediction model based on WT-MIC-GRU—A case study in Dish-Shaped lakes of poyang Lake[J]. Entropy, 2022, 24(4): 457. doi: 10.3390/e24040457 [7] CAO X, REN N, TIAN G, et al. A three-dimensional prediction method of dissolved oxygen in pond culture based on Attention-GRU-GBRT[J]. Computers and Electronics in Agriculture, 2021, 181: 105955. doi: 10.1016/j.compag.2020.105955 [8] 周雪, 鲍刚, 龚顺琦. 基于参数优化的KELM和GRU的短期电力负荷预测[J]. 电子器件, 2022, 45(04): 931-938. doi: 10.3969/j.issn.1005-9490.2022.04.028 [9] 石庆兰, 束金阳, 李道亮, 等. 基于BiLSTM-GRU融合网络的稻虾养殖溶解氧预测方法[J/OL]. 农业机械学报, 2023, 1-9. [10] CHAUHAN A, SHIVAPRAKASH S J, SABIREEN H, et al. Stock price forecasting using pso hypertuned neural nets and ensembling[J]. Applied Soft Computing, 2023, 147: 110835. doi: 10.1016/j.asoc.2023.110835 [11] XIAO Y, ZHANG L. Smart grid energy storage capacity planning and scheduling optimization through PSO-GRU and multihead-attention[J]. Frontiers in Energy Research, 2023, 11: 1254371. doi: 10.3389/fenrg.2023.1254371 [12] 朱菊香, 任明煜, 谷卫, 等. 基于CEEMDAN-IGWO-CNN-LSTM空气质量预测建模[J/OL]. 计算机仿真, 2023, 1-11. [13] KADHUIM Z A, AL-JANABI S. Codon-mRNA prediction using deep optimal neurocomputing technique (DLSTM-DSN-WOA) and multivariate analysis[J]. Results in Engineering, 2023, 17: 100847. doi: 10.1016/j.rineng.2022.100847 [14] MOHAMMED H M, UMAR S U, RASHID T A. A systematic and meta‐analysis survey of whale optimization algorithm[J]. Computational Intelligence and Neuroscience, 2019, 2019(1): 8718571. [15] 李浩, 李浩, 杨扬, 等. 基于改进鲸鱼算法优化GRU的PEMFC老化预测[J/OL]. 中国电机工程学报, 2023, 1-14. [16] 蔡国庆, 刘玲, 张冲, 等. 基于GNN-LSTM-CNN网络的6G车辆轨迹预测算法[J]. 西安电子科技大学学报, 2023, 50(03): 50-60. [17] 苏辉锋, 丁乐声, 王绪旺, 等. 基于CNN-GRU混合模型的养殖工船水体溶解氧预测研究[J]. 南方水产科学, 2023, 19(04): 174-180. doi: 10.12131/20220298 [18] 张丽娜, 陈会娟, 余昭旭. 基于TimeGAN-CNN-LSTM模型的河流水质预测研究[J]. 自动化仪表, 2022, 43(08): 11-15. [19] 陈英义, 程倩倩, 方晓敏, 于辉辉, 李道亮. 主成分分析和长短时记忆神经网络预测水产养殖水体溶解氧[J]. 农业工程学报, 2018, 34(17): 183-191. doi: 10.11975/j.issn.1002-6819.2018.17.024 [20] 李先鹏, 吴若男, 王魏, 李双双. 基于小波降噪和LSTM的海参养殖氨氮预测[J]. 控制工程, 2022, 29(4): 587-592626. [21] 魏伟, 赵小强, 吴进. 基于VMD-ICSO-GRU的高铁列控车载设备故障率时间序列预测[J]. 铁道学报, 2023, 45(6): 58-68. doi: 10.3969/j.issn.1001-8360.2023.06.007 -


 下载:
下载: