-
以煤为主的能源消费结构导致了严重的环境污染。在2018年“全球环境绩效指数”排名中,中国在180个国家中综合得分排名为120位,空气质量排名倒数第4。煤炭燃烧是大气污染的主要来源,虽然散煤在全部煤炭消费中只占大约20%,但是不完全燃烧、缺乏污染物处理装置等因素增大了散煤的治理难度。为了治理大气污染,2013年国务院在“大气十条”中将“煤改气”工程列为加强大气污染综合治理的重要举措,2016年包括京津冀在内的“2+26”城市重点推行“煤改气”工程,取得了良好效果。虽然气代煤可以减少污染物排放,有利于能源消费结构转变,但是,随着“煤改气”工程的推行,用气量大幅增加导致的“气荒”以及高成本等问题逐渐暴露出来。2018年7月3日,国家能源局针对“煤改气”和“煤改电”在推行过程中的种种问题,明确提出要“因地制宜”拓展多种清洁供暖方式,标志着进入后“煤改气”时代。
“煤改气”工程实施以来,国内外学者针对该项政策实施的环境效益和经济效益展开讨论。环境效益方面,大部分学者通过对进行“煤改气”工程前后案例城市的环境质量进行比较分析,认为“煤改气”工程能够显著减少由于燃煤导致的污染物排放,改善环境质量[1-3]。WILSON et al[4]、TANAKA et al[5]、 BERNEY[6]、CHEN et al[7]认为煤改气能够显著减少二氧化碳、二氧化硫等污染排放。经济效益方面,学者们普遍认为实施煤改气会增加企业和居民的成本,煤改气成本远超居民的价格承受能力[8-11]。由于经济性不强,企业和用户对煤改气的执行动力不足,政府补贴成为缓冲附加成本的有效手段。ZHAO et al[12]、杜晓林等[13]、汤燕刚[14]的研究均表明政府补贴能够推动清洁取暖的施行,而刘应红[8]、XU[15]则表示政府补贴效率有待提高。
近年来,博弈论逐渐用于分析政府与企业(居民)之间的策略选择。WANG et al[16]运用博弈理论分析了政府和供热企业之间的策略选择问题,当政府提高补贴和企业利润、减少清洁供暖成本时,有利于煤改清洁能源的推行。张国兴[17]、占华[18]、初钊鹏等[19]利用博弈理论分析了节能减排过程中政府与企业的策略选择。钟太勇[20]、JI[21]运用博弈论分析政府与新能源汽车制造商的策略行为,研究表明政府应采取补贴退坡政策。曹国华等[22]采用演化博弈理论研究了政府补贴如何影响新能源汽车消费者的购买行为。朱庆华[23]和SUN[24]则运用博弈模型分析了绿色供应链管理中政府补贴和厂商的行为。
居民(包括企业)作为清洁取暖工程的主体,是否进行“煤改气”改造对于改变能源消费结构、实现低碳绿色发展具有重要作用;而政府作为政策实施者,如何制定相关激励政策(例如补贴、退税)发挥引导和调节居民行为的作用。政府与居民作为博弈双方的主体相互制约,探究政府与居民行为之间的作用机制对于推进清洁取暖、实现节能减排具有重要作用。本文尝试引入演化博弈论构建居民在不同因素影响下的清洁取暖行为模型,并分析影响动态系统稳定的关键因素。
全文HTML
-
当前,全国各地都对“煤改气”用户进行一定补贴,但是,随着时间的推移,政府的补贴退坡机制将使进行“煤改气”的补贴额度越来越少。假设当有取暖需求的居民(以下称为“消费者”)进行了“煤改气”,得到的政府补贴为ωI,其中ω(%)表示由于补贴退坡机制而随时间变化的补贴率,假设此时政府的社会收益为
$ {{G}}_{{1}} $ ,那么政府的最终收益即社会总福利为$ {G_1} - \omega I$ ;若消费者不进行“煤改气”,由于排放大量污染物需要额外缴纳一部分税收或者罚款$ {T} $ ,此时政府的社会收益为$ {{G}}_{{2}} $ ,那么社会总福利为$ {{G}}_{{2}}+{T} $ 。假设消费者进行“煤改气”后所得到的效应为$ {{U}}_{{1}} $ ,不进行“煤改气”的效应为$ {{U}}_{{2}} $ 。消费者在改造时要考虑各种成本和“煤改气”所能带来的效应。假设进行“煤改气”的设备购置成本、维修成本等各种成本为$ {{C}}_{{1}} $ ,不进行“煤改气”的各种成本为$ {{C}}_{{2}} $ ,另外在“煤改气”工程推行初期,由于各项技术尚未攻关将导致消费者效应损失$ {{U}}_{{s}} $ 。假设消费者选择进行“煤改气”的概率为α,选择不进行“煤改气”的概率为1-α。政府给予消费者财政补贴激励的概率为
$ \beta $ ,不进行财政补贴激励的概率为1-$ \beta $ 。最终得出的消费者与政府的博弈支付矩阵见表1。表1可知,消费者的期望收益可以表示为:
进行“煤改气”:
${{E}}{({\rm{Con}})_\alpha } = \beta \left( {{U_1} - {C_1} - {U_s} + \omega I} \right) +$ $\left( {1 - \beta } \right)\left( {{U_1} - {C_1} - {U_s}} \right) = {U_1} - {C_1} - {U_s} + \beta \omega I$ ,不进行“煤改气”:${{E(Con}}{{\rm{)}}_{1 - \alpha }} = \beta \left( {{U_2} - {C_2} - T} \right) + \left( {1 - \beta } \right)\left( {{U_2} - {C_2}} \right) =$ ${U_2} - {C_2} - \beta T$ 。二者之和为消费者的平均收益见式(1)。
那么消费者的复制动态方程见(2)。
同理可得政府的平均收益见式(3)。
那么政府的复制动态方程为(4)。
-
令
${{F}}\left( \alpha \right){\rm{ = }}\dfrac{{{\rm{d\alpha }}}}{{{\rm{dt}}}}$ ,一阶导数${{F}}'\left( \alpha \right) = \left( {1 - 2\alpha } \right)({U_1} - {C_1} -$ $ {U_s} + \beta \omega I - {U_2} + {C_2} + \beta T)$ ,令${{F}}\left( \alpha \right){\rm{ = }}\dfrac{{{\rm{d\alpha }}}}{{{\rm{dt}}}}{\rm{ = 0}}$ ,解得${\alpha _1}{\rm{ = 0,}}\;\;{\alpha _{\rm{2}}}{\rm{ = 1,}}\;\;{\beta ^*} = \dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2}}}{{\omega I + T}}$ 。根据微分方程稳定性的定义可知,当
${{F}}\left( \alpha \right){\rm{ = }}\dfrac{{{\rm{d\alpha }}}}{{{\rm{dt}}}}{\rm{ = 0}}$ 时,一阶导数${{F}}'\left( \alpha \right) < {\rm{ 0}}$ ,此时α为演化稳定策略。当
${\beta ^*} = \dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2}}}{{\omega I + T}}$ 时,$ {F}\left(\alpha \right){=}{{F}}'\left(\alpha \right){=}{0} $ ,此时消费者选择进行“煤改气”的概率是稳定的,不会因政府补贴或者“煤改气”成本的变化而改变自身状态。具体来说,当${{F}}\left( \alpha \right){{ = F'}}\left( \alpha \right){\rm{ = 0}}$ 时,对于任意α都是一种稳定状态,但并不会经历演化和学习的过程。就“煤改气”而言,如果消费者已经完成了“煤改气”,那么即使政府补贴减少或者“煤改气”成本上升,消费者依然会选择维持当前天然气取暖的状态;如果消费者并没有完成“煤改气”,同样也不会因政府补贴增加、“煤改气”成本降低而改变当前燃煤取暖的状态。即市场上选择燃煤取暖和燃气取暖的消费者比例不会发生任何变化。当
${\beta ^*} \ne \dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2}}}{{\omega I + T}}$ 时:1)若
$\dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2}}}{{\omega I + T}} < 0$ 此时,
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}>{{U}}_{{2}}-{{C}}_{{2}} $ ,即消费者选择进行“煤改气”在没有政府补贴激励的情况下获得的效应大于不进行“煤改气”获得的效应,恒有$\,{\beta ^*} > \dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2}}}{{\omega I + T}}$ ,对于${\alpha _1} = 0,\;\;{\alpha _2} = 1$ ,有${{F}}\left( {\rm{0}} \right){{ = F}}\left( {\rm{1}} \right){\rm{ = 0}},\;\;{{F}}'\left( {\rm{0}} \right){\rm{ > 0,}}\;\;{{F}}'\left( {\rm{1}} \right){\rm{ < 0}}$ ,可知${\alpha _{\rm{2}}}{\rm{ = 1}}$ 为演化稳定策略。即此时无论政府是否选择进行激励,消费者都会选择进行“煤改气”。2)若
$\dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2}}}{{\omega I + T}} = 0$ 此时,
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}{=}{{U}}_{{2}}-{{C}}_{{2}} $ ,即消费者选择进行“煤改气”在没有政府补贴激励的情况下获得的效应等于不进行“煤改气”获得的效应,对于${\alpha _1} = 0, $ ${\alpha _2} = 1$ ,同样有${{{F}}}\left({0}\right){={{F}}}\left({1}\right){=0}$ ,${{{{F}}}}'\left({0}\right){ > 0}$ ,${{{{F}}}}'\left({1}\right){ < 0}$ ,可知$ {\alpha _2} = 1 $ 为演化稳定策略。此种情况下,即便政府不进行补贴激励,消费者仍然会选择进行“煤改气”。3)若
$\dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2}}}{{\omega I + T}} > 1 $ 此时,
${U_1} - {C_1} - {U_s} + \omega I < {U_2} - {C_2} - T$ ,即消费者选择进行“煤改气”在有政府补贴激励的情况下获得的效应小于不进行“煤改气”获得的效应,恒有${\beta ^*} < \dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2}}}{{\omega I + T}}$ ,对于${\alpha _1} = 0,\;\;{\alpha _2} = 1$ ,有${{{F}}}\left({0}\right)=$ ${{{F}}}\left({1}\right){=}{0}$ ,${{{{F}}}}'\left({0}\right){ < 0}$ ,${{{{F}}}}'\left({1}\right){ > 0}$ ,可知${\alpha _1} = 0 $ 为演化稳定策略。此时无论政府补贴额度如何,消费者都不会进行“煤改气”改造。4)若
$\dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2}}}{{\omega I + T}} = 1$ 此时,
${U_1} - {C_1} - {U_s} + \omega I = {U_2} - {C_2} - T$ ,即消费者选择进行“煤改气”在有政府补贴激励的情况下所获得的效应等于不进行“煤改气”获得的效应,对于${\alpha _1} = 0,\;\;{\alpha _2} = 1$ ,有${{{F}}}\left({0}\right){={{F}}}\left({1}\right){=}{0}$ ,${{{{F}}}}'\left({0}\right){ < 0}$ ,${{{{F}}}}'\left({1}\right){ > 0}$ ,可知${\alpha _1} = 0$ 为演化稳定策略。此时无论政府补贴额度如何,消费者都不会进行“煤改气”改造。5)若
$0 < \dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2}}}{{\omega I + T}} < 1$ 此时,
${U_1} - {C_1} - {U_s} < {U_2} - {C_2},\;\;{U_1} - {C_1} - {U_s} + \omega I > $ ${U_2} -{C_2} - T$ ,消费者选择进行“煤改气”在没有政府补贴激励的情况下所获得的效应小于不进行“煤改气”获得的效应,但是在有政府补贴激励的情况下所获得的效应要大于不进行“煤改气”获得的效应。可以分为两种情况:①当
$\,{\beta ^*} \!<\! \dfrac{{{U_2}\! + {U_s} \!+ {C_1} - {U_1} - {C_2}}}{{\omega I + T}}$ ,对于${\alpha _1} = 0, $ ${\alpha _2} = 1$ ,有${{{F}}}\left({0}\right){={{F}}}\left({1}\right){=}{0}$ ,${{{{F}}}}'\left({0}\right){ < 0}$ ,${{{{F}}}}'\left({1}\right){ > 0}$ ,可知${\alpha _1} = 0$ 为演化稳定策略。此时,$ \omega I < \dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2} - {\beta ^*}T}}{{{\beta ^*}}}$ ,即当政府对消费者进行“煤改气”的补贴ωI低于$\dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2} - {\beta ^*}T}}{{{\beta ^*}}}$ 时,消费者进行“煤改气”的概率将降低,不进行“煤改气”是其最优策略选择。②当
$\,{\beta ^*} \! > \!\dfrac{{{U_2} +\! {U_s} +\! {C_1} - {U_1} - {C_2}}}{{\omega I + T}}$ ,对于$ {\alpha _1} = 0 $ ,$ {\alpha _2} = 1 $ ,有${{{F}}}\left({0}\right){={{F}}}\left({1}\right){=}{0}$ ,${{{{F}}}}'\left({0}\right){ > 0}$ ,${{{{F}}}}'\left({1}\right){ < 0}$ ,可知$ {\alpha _2} = 1 $ 为演化稳定策略。此时,$\omega I > \dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2} - {\beta ^*}T}}{{{\beta ^*}}}$ ,即当政府对消费者进行“煤改气”的补贴ωI高于$\dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2} - {\beta ^*}T}}{{{\beta ^*}}}$ 时,消费者进行“煤改气”的概率将提升,进行“煤改气”是其最优策略选择。根据以上分析,可以得到消费者的演化规律,消费者的复制动态相位图见图1。
-
令
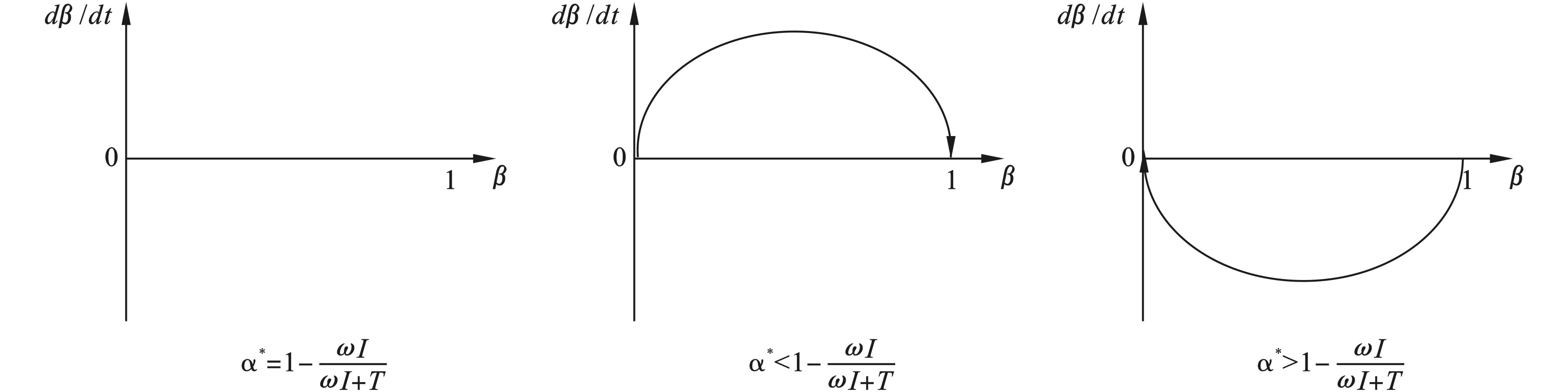
${{F}}\left( \beta \right){\rm{ = }}\dfrac{{{\rm{d \beta }}}}{{{\rm{dt}}}}$ ,一阶导数${{F}}'\left( {\rm{\beta }} \right){\rm{ = }}\left( {1 \!-\! 2\beta } \right)(T\! -\! \alpha T\! -\! \alpha \omega I)$ ,令${{F}}\left( \beta \right){\rm{ = }}\dfrac{{{\rm{d\beta }}}}{{{\rm{dt}}}}{\rm{ = 0}}$ ,解得${\beta _{\rm{1}}}{\rm{ = 0}}$ ,$ {\beta _2}{\rm{ = 1}} $ ,${\alpha ^*} = 1 - \dfrac{{\omega I}}{{\omega I + T}}$ 。根据微分方程稳定性的定义可知,当
${{F}}\left( \beta \right){\rm{ = }}\dfrac{{{\rm{d\beta }}}}{{{\rm{dt}}}}{\rm{ = 0}}$ 时,一阶导数${{F}}'\left( \beta \right){\rm{ < 0}}$ ,β为演化稳定策略。当
${\alpha ^*} = 1 - \dfrac{{\omega I}}{{\omega I + T}}$ 时,${{F}}\left( \beta \right) = {{F}}'\left( \beta \right){\rm{ = 0}}$ ,此时政府选择对“煤改气”进行补贴的概率是稳定的,此时同样不会发生演化的过程。当
${\alpha ^*} \ne 1 - \dfrac{{\omega I}}{{\omega I + T}}$ 时,因为$\omega I > 0,\;\;T > 0$ ,所以$0 < 1 - \dfrac{{\omega I}}{{\omega I + T}} < 1$ 。同理此时也可以分为以下两种情况讨论:若
$ {\alpha ^*} < 1 - \dfrac{{\omega I}}{{\omega I + T}}$ ,对于$ \,{\beta _1} = 0 $ ,$ \,{\beta _2} = 1 $ ,有${{{F}}}\left({0}\right){={{F}}}\left({1}\right){=}{0}$ ,${{{{F}}}}'\left({0}\right){ > 0}$ ,${{{{F}}}}'\left({1}\right){ < 0}$ ,可知$ {\beta _2} = 1 $ 为演化稳定策略。即当消费者进行“煤改气”的概率小于$1 - \dfrac{{\omega I}}{{\omega I + T}}$ 时,政府选择进行补贴是其最优策略。若
${\alpha ^*} > 1 - \dfrac{{\omega I}}{{\omega I + T}}$ ,对于$ \,{\beta _1} = 0 $ ,$ \,{\beta _2} = 1 $ ,有${{{F}}}\left({0}\right){={{F}}}\left({1}\right){=}{0}$ ,${{{{F}}}}'\left({0}\right){ < 0}$ ,${{{{F}}}}'\left({1}\right){ > 0}$ ,可知$ {\beta _2} = 0 $ 为演化稳定策略。即当消费者进行“煤改气”的概率大于$ 1 - \dfrac{{\omega I}}{{\omega I + T}}$ 时,政府选择不进行补贴是其最优策略。根据以上分析,可以得到政府的演化规律,政府的复制动态相位图见图2。
2.1. 消费者的演化趋势
2.2. 政府的演化趋势
-
根据政府和消费者的复制动态和演化趋势,可知二者组成的动态系统在平面
${{S = }}\left\{ {\left( {\alpha ,\beta } \right);0 \leqslant \alpha ,\beta \leqslant 1} \right\}$ 上有5个局部均衡点,分别为(0,0)、(1,0)、(0,1)、(1,1)和(${\alpha ^*} = 1 - \dfrac{{\omega I}}{{\omega I + T}}$ ,$\,{\beta ^*} = \dfrac{{{U_2} + {U_s} + {C_1} - {U_1} - {C_2}}}{{\omega I + T}}$ ),其中$ {\alpha ^*} \in [0,1]$ ,$\, {\beta ^*} \in [0,1] $ 。该动态系统的稳定性可由Jacobi矩阵的局部稳定性分析得到,由式(2)和(4)组成的Jacobi矩阵为:对应的行列式(Det)、迹(Tr)分别为:
上述5个均衡点对应的
${\rm{Det}}\left( {{J}} \right)$ 和${\rm{Tr}}\left( {{J}} \right)$ 的值见表2。比较消费者在有补贴激励和没有补贴激励下,进行“煤改气”所获得的效应,可知当
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}>{{U}}_{{2}}-{{C}}_{{2}} $ 时,恒有${U_1} - {C_1} - {U_s} + \omega I > {U_2} - {C_2} - T$ ,同理,当${U_1} - {C_1} - {U_s} + \omega I < {U_2} - {C_2} - T$ 时,恒有${U_1} - {C_1} - $ ${U_s} < {U_2} - {C_2}$ ,所以系统的动态稳定性只需分析在$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}>{{U}}_{{2}}-{{C}}_{{2}} $ 和${U_1} - {C_1} - {U_s} + \omega I < {U_2} -{C_2} - T $ 时的结果。 -
此时消费者选择进行“煤改气”在没有政府政策激励下所获得的效应大于其不进行“煤改气”所获得的效应,即无论政府是否施行补贴退坡机制、退坡幅度如何,都不会影响消费者选择进行“煤改气”的策略。变换之后得
$ {{U}}_{{1}}-{{U}}_{{s}}-{{U}}_{{2}}>{{C}}_{{1}}-{{C}}_{{2}} $ ,此时消费者进行“煤改气”所获得的效应$ {{U}}_{{1}} $ 减去因为“煤改气”推行初期诸多技术尚未攻关而导致的效应损失$ {{U}}_{{s}} $ ,得到进行“煤改气”的总效应($ {{U}}_{{1}}-{{U}}_{{s}} $ ),与不进行“煤改气”所获得的效应之差$ {(}{{U}}_{{1}}-{{U}}_{{s}}-{{U}}_{{2}}{)} $ 要大于进行“煤改气”前后成本总和之差($ {{C}}_{{1}}-{{C}}_{{2}} $ )。在此情形下,无论政府始终全额补贴还是实行补贴退坡机制,抑或对不进行“煤改气”的消费者进行罚款或额外征税,消费者都会选择进行“煤改气”,而且这种策略选择是稳定的。最终经过博弈双方的学习和演化,消费者选择进行“煤改气”,政府选择不对进行“煤改气”的消费者进行财政补贴激励,系统趋向于局部稳定均衡点(1,0)。稳定性分析结果见表3。 -
此时消费者选择进行“煤改气”在有补贴激励下所获得的效应小于其不进行“煤改气”的效应,也就是说即便政府对全部进行“煤改气”的消费者进行一定程度的财政激励,消费者依然不会改变自身行为而进行“煤改气”改造。变换之后得
$ \omega I+{T}<$ ${{U}}_{{2}}-{{C}}_{{2}}{-(}{{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}{)} $ ,此时政府的正向激励(财政补贴)和负向激励(罚款或额外征税)之和小于消费者在没有财政激励时不进行“煤改气”的效应与进行“煤改气”所获得的效应之差,说明政府的财政激励力度仍然不能促进消费者改变原先的取暖模式而进行清洁取暖,所以此时系统趋向于局部稳定均衡点(0,1)。稳定性分析结果见表4。 -
此时
$ {0<}\dfrac{{{U}}_{{2}}+{{U}}_{{s}}+{{C}}_{{1}}-{{U}}_{{1}}-{{C}}_{{2}}}{\omega I+{T}}{<1} $ ,消费者选择进行“煤改气”在受到政府的补贴激励下所获得的效应大于其不进行“煤改气”所获得的效应,在没有政府的补贴激励下进行“煤改气”所获得的效应小于不进行“煤改气”所获得的效应。依据$ {\alpha }^{{*}} $ 值的不同,分为以下两种情况。当
$ {\alpha }^{{*}}<{1-}\dfrac{\omega I}{\omega I+{T}} $ ,政府选择对进行“煤改气”的消费者进行财政补贴激励时,消费者将选择进行“煤改气”,对应均衡点(1,1);当
$ {\alpha }^{{*}}>{1-}\dfrac{\omega I}{\omega I+{T}} $ ,政府不对进行“煤改气”的消费者进行财政补贴激励时,消费者将不会进行“煤改气”改造,对应均衡点$ {(0},\;{0)} $ 。所以当
$ {0<}\dfrac{{{U}}_{{2}}+{{U}}_{{s}}+{{C}}_{{1}}-{{U}}_{{1}}-{{C}}_{{2}}}{\omega I+{T}}{<1} $ 时,消费者的策略选择在进行“煤改气”和不进行“煤改气”之间变换,且具备一定不确定性,所以上述两个均衡点(1,1)和$ {(0},\;{0)} $ 并不是稳定的均衡点。令
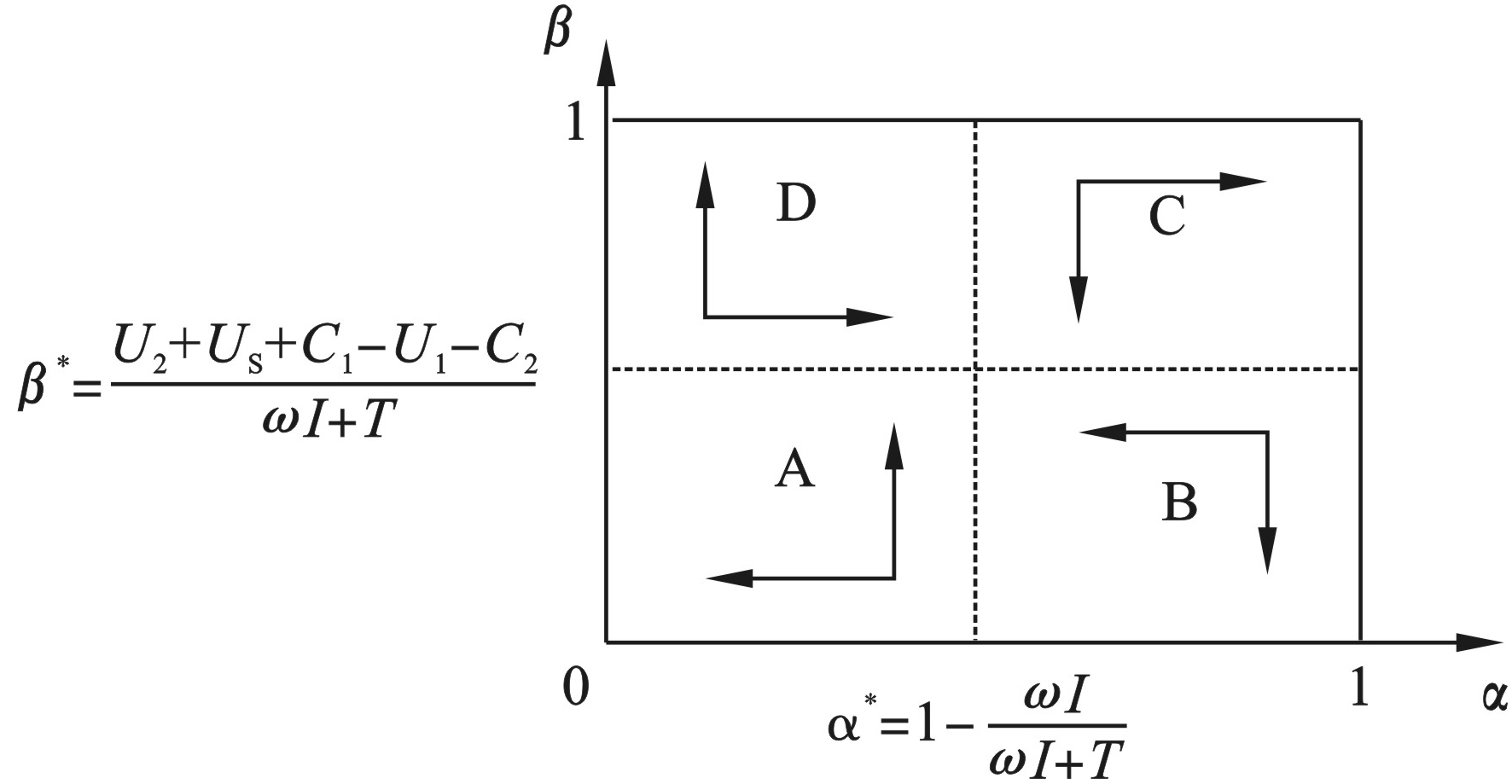
$ {\alpha }^{{*}}{=1-}\dfrac{\omega I}{\omega I+{T}} $ ,$ \,{\beta }^{{*}}{=}\dfrac{{{U}}_{{2}}+{{U}}_{{s}}+{{C}}_{{1}}-{{U}}_{{1}}-{{C}}_{{2}}}{\omega I+{T}} $ ,可以得到消费者与政府策略变化的动态演化趋势,见图3。图3可见,当
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}+\omega I<{{U}}_{{2}}-{{C}}_{{2}}-{T} $ ,恒有$ {\,\beta }^{{*}}<\dfrac{{{U}}_{{2}}+{{U}}_{{s}}+{{C}}_{{1}}-{{U}}_{{1}}-{{C}}_{{2}}}{\omega I+{T}} $ ,对应图3中的区域A和B,此时演化稳定策略为α=0,能够证明当$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}+\omega I<{{U}}_{{2}}-{{C}}_{{2}}-{T} $ 时,消费者不会进行“煤改气”,且消费者的这种选择不依赖于政府的策略变化。当$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}{>{U}}_{{2}}-{{C}}_{{2}} $ ,恒有$ {\beta }^{{*}}>\dfrac{{{U}}_{{2}}+{{U}}_{{s}}+{{C}}_{{1}}-{{U}}_{{1}}-{{C}}_{{2}}}{\omega I+{T}} $ ,对应图3中的区域C和D,此时演化稳定策略为$ \alpha = 1 $ ,也证明了当$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}{>{U}}_{{2}}-{{C}}_{{2}} $ 时,消费者将选择进行“煤改气”,且消费者的这种选择不依赖于政府的策略变化。当$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}+\omega I>{{U}}_{{2}}-{{C}}_{{2}}-{T} $ ,$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}< $ ${{U}}_{{2}}-{{C}}_{{2}},\;{0<}{1}-\dfrac{\omega I}{\omega I+{T}}{<1}$ ,此时消费者选择进行“煤改气”在受到政府财政补贴激励下所获得的效应大于其不进行“煤改气”所获得的效应,而在没有财政补贴激励下进行“煤改气”所获得的效应较小,此时并不存在演化稳定策略。经过演化稳定性分析,可知系统存在(1,0)和(0,1)两个均衡点,其中(1,0)代表的策略组合(进行“煤改气”改造,不进行财政补贴激励)能够实现社会福利最大化。现实条件下,政府和消费者双方都应该采取必要措施使此种策略组合的概率增加。
3.1.
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}>{{U}}_{{2}}-{{C}}_{{2}} $![]()
![]()
3.2.
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}+\omega I<{{U}}_{{2}}-{{C}}_{{2}}-{T} $![]()
![]()
3.3.
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}+\omega I>{{U}}_{{2}}-{{C}}_{{2}}-{T} $![]()
![]()
且$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}< $![]()
![]()
${{U}}_{{2}}-{{C}}_{{2}}$![]()
![]()
-
下面运用Matlab R2016a对上述演化博弈进行数值仿真。横轴和纵轴分别代表消费者选择进行“煤改气”的概率α和政府对进行“煤改气”的消费者采取财政补贴激励的概率β。为全面分析政府和消费者策略选择的变化,对以下五种情形进行数值仿真,其中情形1、情形2、情形3为进行“煤改气”前后消费者收益不相等的情形,情形4、情形5为进行“煤改气”前后消费者收益不受损的情形。
-
对应
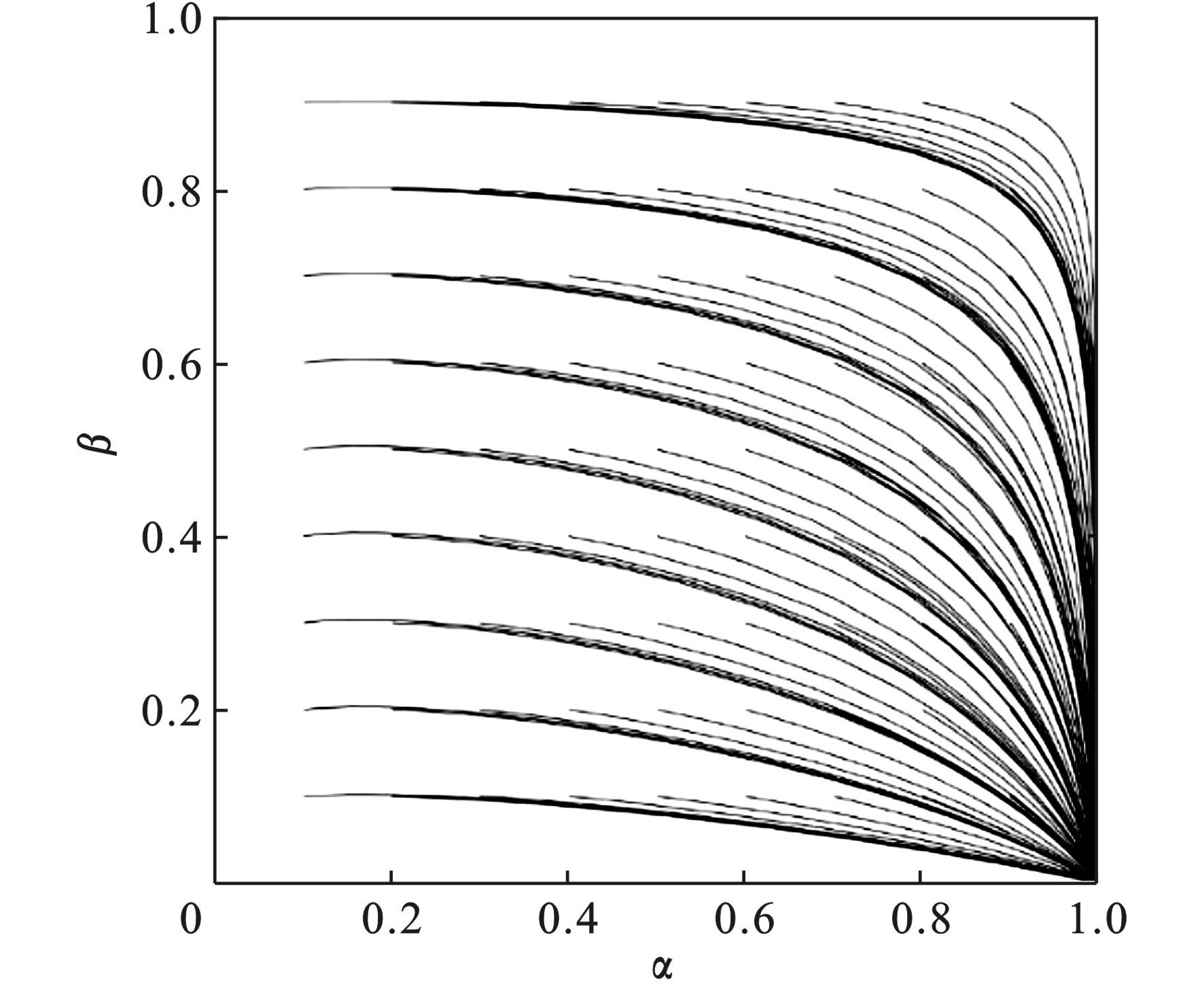
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}>{{U}}_{{2}}-{{C}}_{{2}} $ ,设参数$ {{U}}_{{1}} $ =30,$ {{C}}_{{1}} $ =10,$ {{U}}_{{s}} $ =5,$ {{U}}_{{2}} $ =25,$ {{C}}_{{2}} $ =15,$ {I} $ =10,$ \omega $ =50%,$ {T} $ =1。数值仿真结果见图4。图4显示演化稳定策略为(1,0),即(进行“煤改气”改造,不进行财政补贴激励)。分析不同的初始点[α,β]逐渐向均衡点演化的轨迹:当α的初始值较小时,首先在保持β的同时迅速提高α的值,其次共同降低β的值,最终趋向稳定均衡点(1,0)。这种情形下,起初整个群体中几乎没有消费者主动进行“煤改气”改造,然而由于政府的财政补贴激励,“煤改气”之后的收益明显高于使用散煤取暖的收益,消费者逐渐放弃燃烧散煤而迅速转向“煤改气”,由于市场化竞争初步形成,政府便取消补贴机制。
-
对应
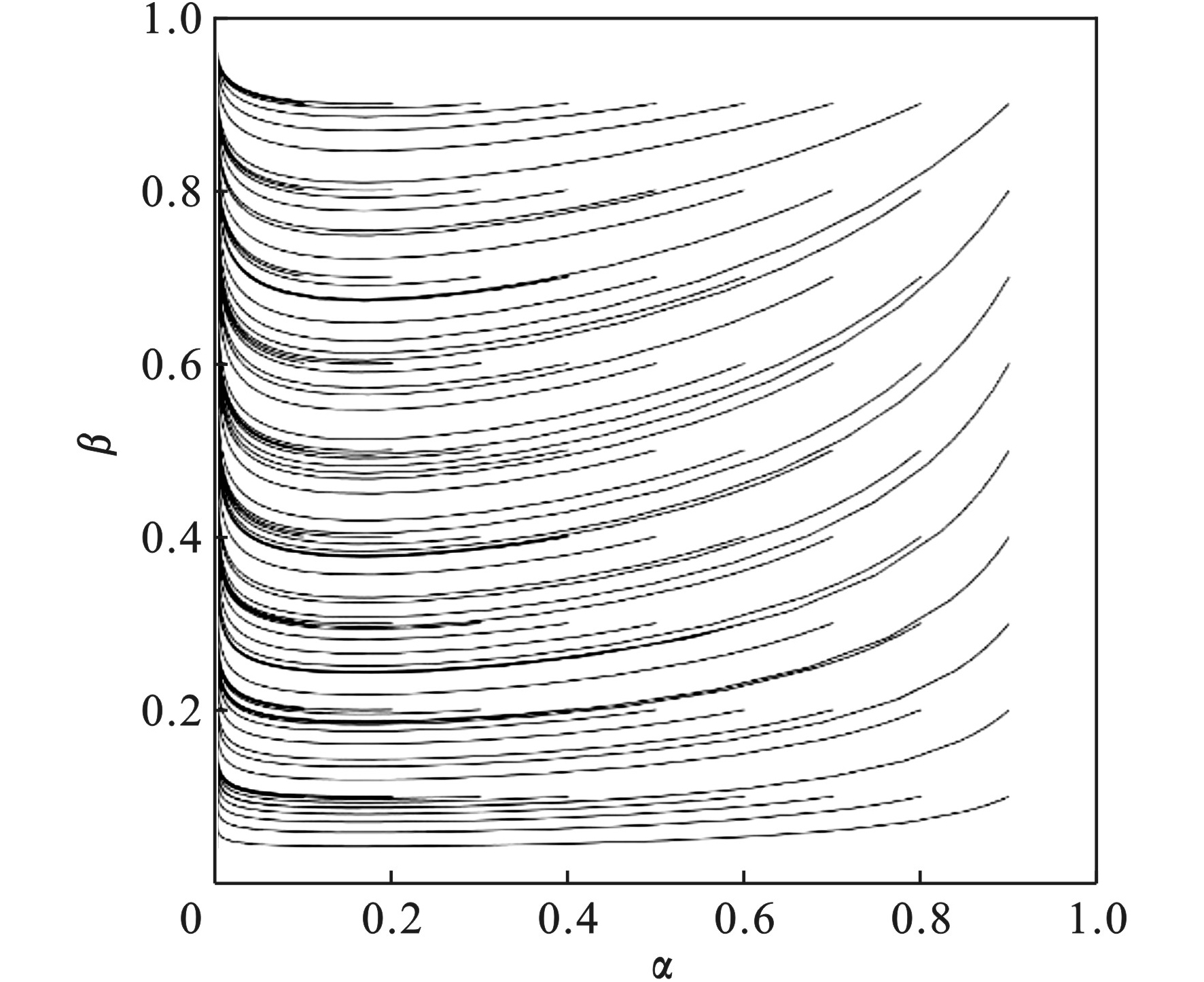
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}+\omega I<{{U}}_{{2}}-{{C}}_{{2}}-{T} $ ,设参数$ {{U}}_{{1}} $ =35,$ {{C}}_{{1}} $ =10,$ {{U}}_{{s}} $ =5,$ {{U}}_{{2}} $ =40,$ {{C}}_{{2}} $ =10,$ {I} $ =10,$ \omega $ =50%,$ {T} $ =1。数值仿真结果见图5。图5显示演化稳定策略为(0,1),即(不进行“煤改气”改造,进行财政补贴激励)。分析不同的初始点[α,β]逐渐向均衡点演化的轨迹:当α的初始值较大时,同样在保持β的同时迅速降低α的值,然后共同提高β的值,最终趋向稳定均衡点(0,1)。这种情形下,起初群体中有一定比例的消费者主动进行“煤改气”改造,然而由于投入成本过高、气-煤价差等问题导致进行“煤改气”之后的收益明显低于散煤取暖的收益,消费者宁愿放弃政府财政激励而继续燃烧散煤,政府为了推动清洁取暖政策,会采取大幅提高财政补贴的措施。
-
对应
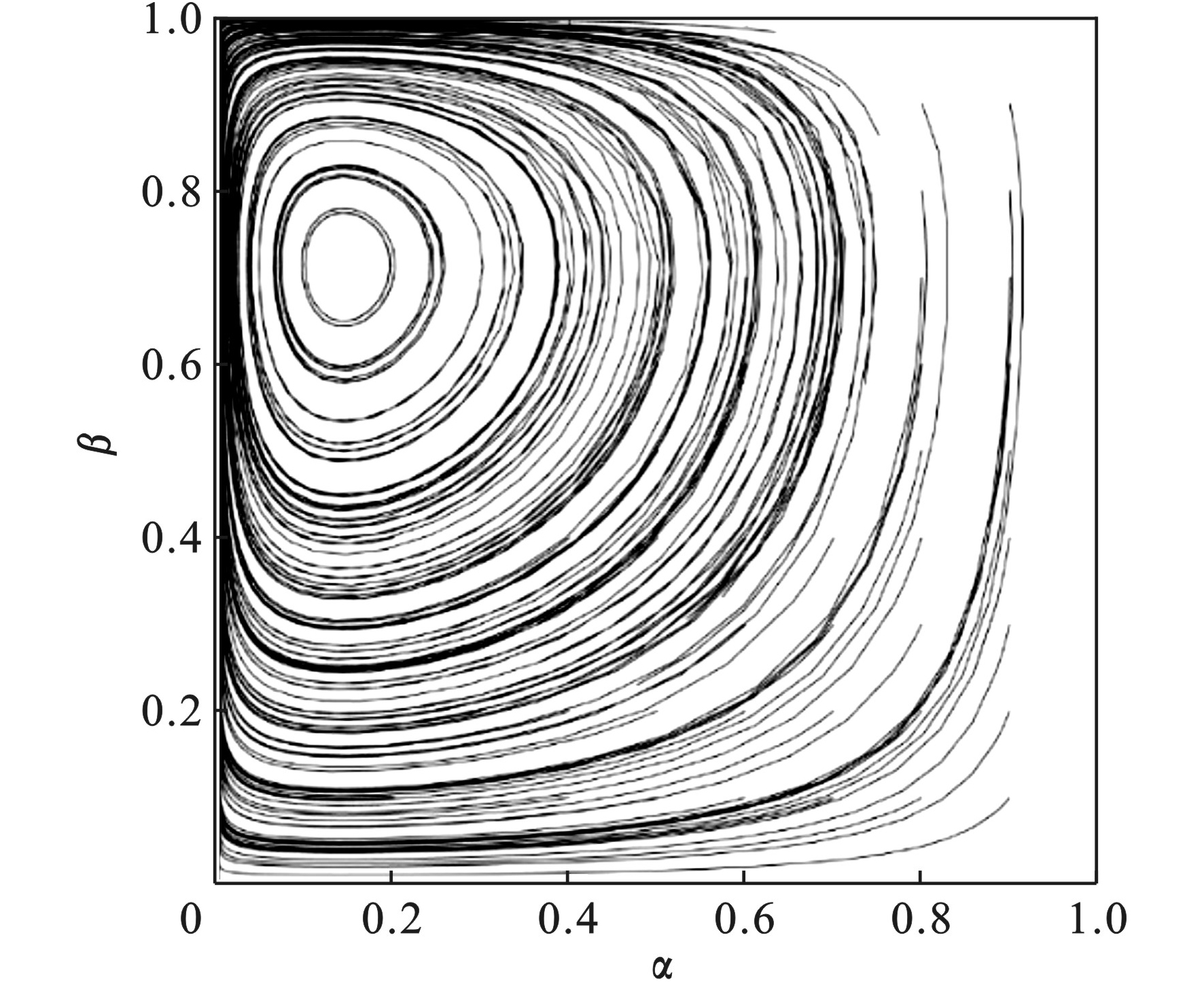
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}+\omega I>{{U}}_{{2}}-{{C}}_{{2}}-{T} $ 且$ {{U}}_{{1}}-{{C}}_{{1}}- $ ${{U}}_{{s}}<{{U}}_{{2}}-{{C}}_{{2}}$ ,设参数$ {{U}}_{{1}} $ =30,$ {{C}}_{{1}} $ =10,$ {{U}}_{{s}} $ =5,$ {{U}}_{{2}} $ =25,$ {{C}}_{{2}} $ =5,$ {I} $ =10,$ \omega $ =60%,$ {T} $ =1。数值仿真结果见图6。图6显示系统并不存在演化稳定策略,只得到中心点(0.14,0.71),说明政府和消费者在策略选择上不是相互独立的,必然具有一定依赖性和周期性。不同的初始点[α,β]动态演化的轨迹:当初始值α小于0.14时,β值朝着1的方向演化;当初始值α大于0.14时,β值朝着0的方向演化。另外,当初始值β小于0.71时,α值朝着0的方向演化;当初始值
$ \beta $ 大于0.71时,α值朝着1的方向演化。在政府公共政策实施过程中,大多数情况会呈现这种状态,也符合经济发展的规律。 -
对应
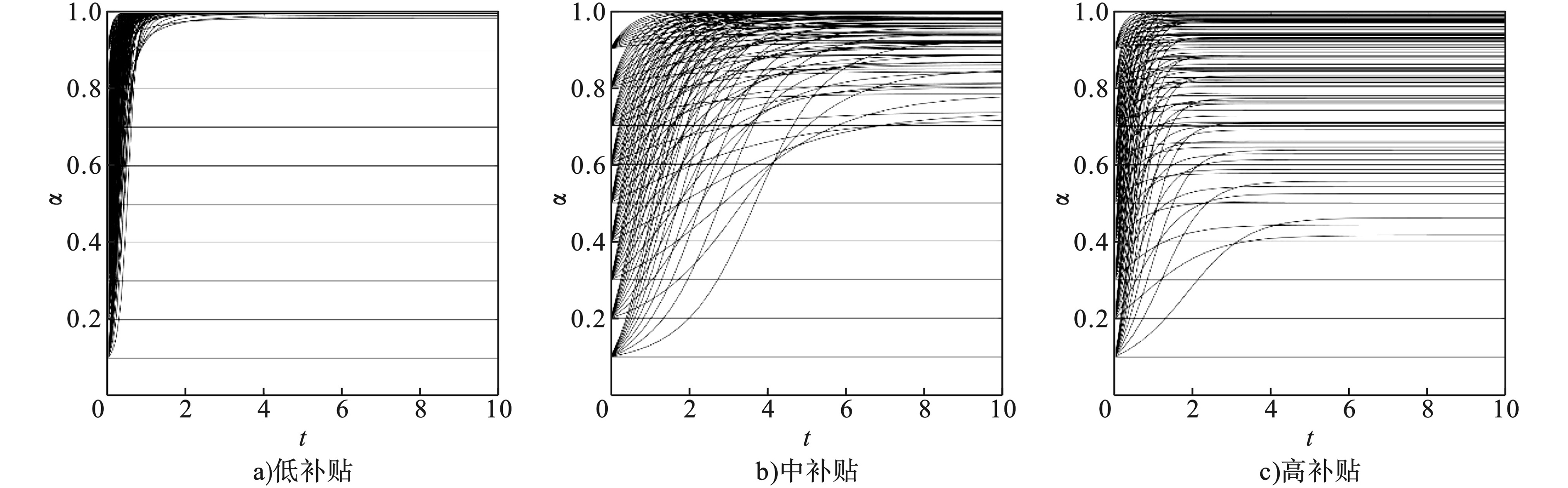
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}{=}{{U}}_{{2}}-{{C}}_{{2}} $ ,设参数$ {{U}}_{{1}} $ =30,$ {{C}}_{{1}} $ =10,$ {{U}}_{{s}} $ =5,$ {{U}}_{{2}} $ =20,$ {{C}}_{{2}} $ =5。根据政府正向补贴激励和负向征税罚款的比例,分别设置低补贴($ \omega I{:}{T}{=1:9} $ )、中补贴($ \omega I{:}{T}{=1:1} $ )、高补贴($ \omega I{:}{T}{=4:1} $ )3种参数进行数值仿真,初始值α随时间t的演化过程见图7。与前面几种情形不同的是,政府进行财政补贴激励的比例β最终趋向0,随着补贴比例逐渐升高,β达到稳定的时间越来越短(由于篇幅问题,此处未给出整体演化图以及β随时间t的演化图)。与此同时,当补贴比例较低时,消费者进行“煤改气”的比例α会在短时间内迅速达到稳定值1,但是随着补贴比例的升高,α达到稳定状态的时间逐渐延长,并且,有较大比例的消费者选择“煤改气”的意愿有所降低。
在没有政府财政补贴激励的情形下,起初群体中有不同比例的消费者主动进行“煤改气”,由于技术进步、市场发展,消费者在“煤改气”之后得到的相对收益比燃煤取暖更高,所以消费者并不依赖政府那部分小额补贴,但是如果部分地区补贴比例很高,消费者为获取政府给予的额外收益,进一步节约成本,便会改变自身策略,导致消费者“煤改气”意愿降低。在现实生活中,此种情形对应于“煤改气”推广后期,由于相关技术的突破,消费者燃气取暖的体验感越来越好,另外,天然气价格进一步改革,加上市场化导致的设备价格降低,燃气取暖的成本不再是阻碍消费者进行“煤改气”的因素。同时,由于居民环保意识的提高和环境规制政策的推行,消费者必然会倾向于进行“煤改气”。在这个过程中,政府必须根据不同地区的现实条件确定适当的补贴比例,避免消费者产生不平衡心理。
-
对应
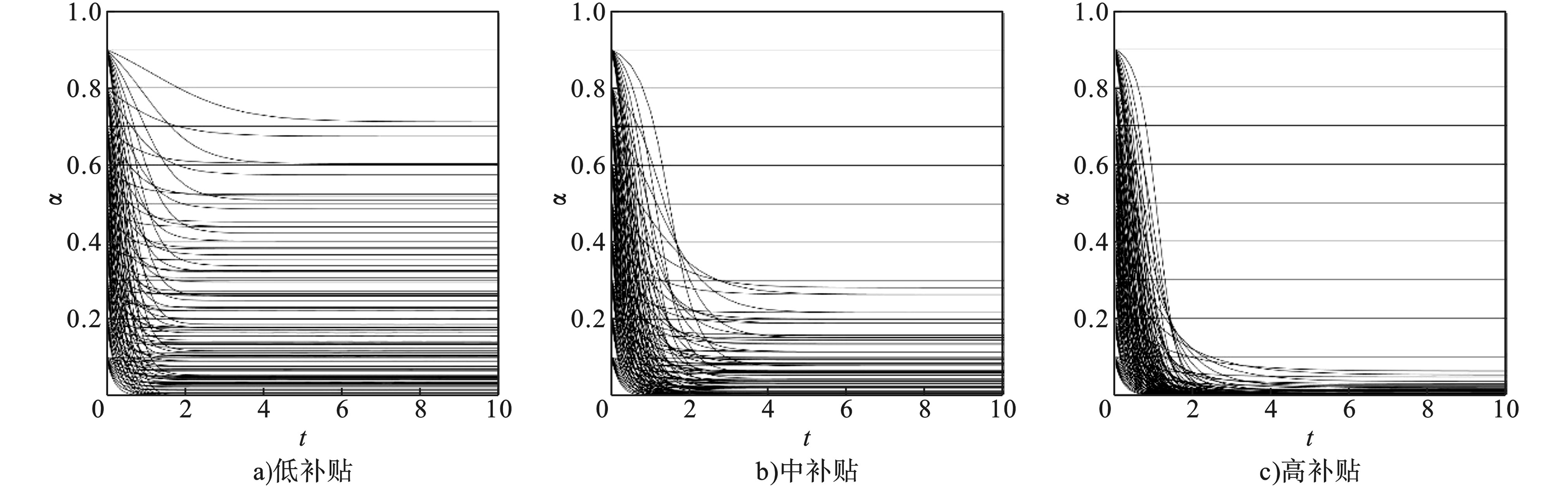
$ {{U}}_{{1}}-{{C}}_{{1}}-{{U}}_{{s}}+\omega I{=}{{U}}_{{2}}-{{C}}_{{2}}-{T} $ ,设参数$ {{U}}_{{1}} $ =30,$ {{C}}_{{1}} $ =10,$ {{U}}_{{s}} $ =5,$ {{U}}_{{2}} $ =25,$ {{C}}_{{2}} $ =5。同样根据政府正向补贴激励和负向征税罚款的比例,分别设置低补贴($ \omega I{:}{T}{=1:9} $ )、中补贴($ \omega I{:}{T}{=1:1} $ )、高补贴($ \omega I{:}{T}{=4:1} $ )3种参数进行数值仿真,初始值α随时间t的演化过程见图8。与情形4相反,此种情形下β最终趋向1,但是随着正向补贴激励的比例逐渐升高,β达到稳定的时间越来越长。与此同时,当补贴比例较低时,α并不会迅速趋向于稳定值1,而是不同程度的降低,但是随着补贴比例的升高,α达到稳定状态的时间逐渐缩短,并且,有较大比例的消费者选择“煤改气”的意愿有所降低,系统逐渐趋向于稳定策略(0,1)。
在有政府财政补贴激励时,起初群体中同样有不同比例的消费者主动进行“煤改气”,但是由于改造成本太高,消费者只有在获取政府补贴的情形下才能保证自身收益不受损。另外,政府补贴金额实际上是成本的一种反映,补贴比例越高,说明燃气取暖成本没有优势,消费者必然不会选择进行“煤改气”。在现实生活中,此种情形对应于“煤改气”推广前期,此时相关技术不成熟,天然气价格居高不下,市场化机制尚未形成,成本问题将会成为阻碍消费者进行“煤改气”的关键因素。因此在推广前期,政府应及时实施相关支持政策,适当提高补贴比例,提升消费者对“煤改气”的认同感,避免“煤改气”政策的夭折。
4.1. 情形1:无补贴,消费者高收益
4.2. 情形2:有补贴,消费者低收益
4.3. 情形3:有补贴,消费者高收益;无补贴,消费者低收益
4.4. 情形4:无补贴,消费者收益不受损
4.5. 情形5:有补贴,消费者收益不受损
-
本文运用演化博弈理论研究了消费者进行“煤改气”改造的策略选择和政府对“煤改气”进行财政补贴激励的策略选择的互动机制,得出如下结论。
1)对于消费者而言,如果进行“煤改气”改造的收益较高(高于散煤取暖),无论政府是否进行财政补贴激励,消费者一定会选择“煤改气”策略。在这种消费者的决策行为下,政府一定会选择不进行财政补贴激励策略。
2)对于政府而言,如果对“煤改气”进行财政激励的收益较低,无论消费者是否进行“煤改气”改造,政府一定会选择不对消费者进行财政补贴激励的策略。在这种政府的决策行为下,一旦散煤取暖的收益高于进行“煤改气”,消费者为实现效用最大化必然选择散煤取暖,因此,消费者并不会主动选择进行“煤改气”改造。
3)最终结果显示系统存在两个演化稳定状态,分别是消费者选择进行“煤改气”,政府选择不对进行“煤改气”的消费者进行财政补贴激励;消费者不进行“煤改气”,政府选择对进行“煤改气”的消费者进行财政补贴激励。其中,只有消费者选择进行“煤改气”,政府选择不对进行“煤改气”的消费者进行财政补贴激励的演化策略才会达到社会福利最大化的目标。
因此,为提升消费者清洁取暖的效用,推动“煤改气”工程的实施,提出以下几点建议。
1)政府应鼓励企业对燃气炉进行技术创新和改造,降低居民清洁取暖的改造成本。燃气炉、天然气管道等基础设施是进行清洁取暖所必需的,其完善性和经济性是推动“煤改气”发展的重要基础,政府可以对相关企业适当激励,给予财政补贴或者税收优惠,引导企业主动技术创新,对燃气炉等基础设施进行投资,从而减少消费者由于推行“煤改气”初期的技术难题而产生的效应损失,增加消费者进行“煤改气”改造的概率。
2)持续推进天然气市场化改革,缩小气-煤价差,进一步降低居民清洁取暖成本。有调研数据表明“煤改气”、“煤改电”之后的取暖成本是燃烧散煤的3倍左右,如果政府取消补贴,居民大多表示“将再使用燃煤取暖”。成本问题无疑是阻碍“煤改气”推行的最大障碍。而天然气市场化改革的重中之重——价格改革,逐步实现国内天然气价格的市场化,健全相关法律制度,推行第三方准入,促进市场多元化竞争。
3)因地制宜推行“煤改气”,避免“一刀切”。虽然“煤改气”能够有效改善北方地区的空气质量,但是“一刀切”限煤措施导致多地天然气供需矛盾突出,2017年采暖季以来发生多次“气荒”,不仅影响居民的取暖,更减少了工业用气,阻碍了整个市场的发展。政府应在解决气源问题的基础上,根据各地发展情况,因地制宜推行清洁取暖,不能急躁冒进。
4)加强宣传,提升居民对“煤改气”等清洁取暖的认同感。大气污染、雾霾频发严重影响了居民的日常生活和身体健康,通过有效的宣传手段将“煤改气”政策与提升空气治理、降低雾霾发生率、有效节能减排联系在一起,能够提升居民对清洁取暖的认同感和偏好,使“煤改气”为代表的清洁取暖得到进一步推广和普及。


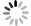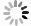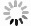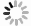
 下载:
下载: