-
有机物是化工、石油加工等行业的主要生产原料，渗入土壤中会造成严重地下水污染[1]. 目前，工业活动和意外泄漏导致我国约90%的城市地下水遭受不同程度有机污染，对水质和含水层生态系统造成严重威胁[2 − 3]. 欧洲环境署表示，矿物油等有机污染物是欧洲地下水污染的主要来源[4]. 甲苯和三氯乙烯作为苯系物和氯代烃中的典型污染物，广泛存在于地下水环境中. 地下水中有机污染物的最终归宿受对流弥散、传质作用以及吸附衰减控制[5]，地下水环境因素的复杂性，影响其在含水层中分布. 为探究有机污染物迁移的关键影响参数，人们对不同条件下污染物迁移进行了大量实验和模拟研究，静态吸附实验探究了污染物吸附特征及影响因素[6]，一维土柱实验侧重于探究污染物沿水流方向迁移规律[7]，二维槽试验主要探究二维体系下污染物在对流弥散、吸附等作用下纵向和横向的迁移特征[8]. 但多依赖于室内小试试验，而实际场地污染物发生多维度迁移，导致其迁移规律与实际迁移过程存在较大差异. 为摆脱尺度效应的影响更贴近真实场地，构建多维度大规模试验装置对污染物迁移过程进行测试，三维槽试验比一维和二维实验更能反映污染场地的迁移特征，同时大型试验装置可有效降低边壁效应及数值模拟误差带来的影响，因此有必要创新性的构建大型地下水试验装置进行复合污染物迁移过程模拟，探究影响其迁移性能的关键因素.
数值模拟已成为模拟地下水流动和溶质运移的重要工具，早期地下水模拟多采用电类比法，20世纪60年代逐步过渡为数值法，20世纪70年代以来三维水流模型和有限元法的引入，使相继开发的GMS、Visual MODFLOW、FEFLOW、Visual Groundwater等地下水数值模拟软件飞速发展，并在20世纪90年代末陆续引入我国，后在21世纪初被广泛运用于我国污染物迁移模拟预测、地下水资源管理及风险评估等方面的研究[9]. GUO等[10]利用Visual MODFLOW和MT3DMS探究制革厂污染物的时空分布特征，结果表明受水文地质限制，水中Cr呈现上升后稳定或下降的趋势. Zhao等[11]利用GMS软件模拟垃圾渗滤液的迁移情况，综合评价发现研究区内40%以上的地下水处于高风险区域. 刘玲等[12]利用FEFLOW模型，定量描述污染场地Cr在土壤-地下水中的迁移规律. 在数值模拟过程中，地下水环境的复杂性和不可见性使模型参数具有不确定性，间接导致模拟结果不确定性[13]. 敏感性分析是建立和改进数学模型的重要工具，具有量化不确定性和度量敏感性的功能[14 − 15]，反映参数变化对不确定性的影响程度[16 − 18]. 敏感度分析方法可分为局部和全局两类[19]. 局部灵敏性分析是在参数值范围内评价参数灵敏度[20]，全局敏感性分析量化所有参数不确定性贡献率[21]. WANG等[22]基于沙箱建立的溶质运移模型，采用局部分析法得到影响迁移的敏感参数大小依次为：弥散度、孔隙度和导水率. SONG等[23]指出全局敏感性分析使模型模拟数据大量输入，具有运行周期长、准确性低等问题，需降低参数维度减少噪声，优化模型计算成本. 张冠儒等[24]将正交试验法用于宝鸡峡灌区，分析表明地表水灌溉量和蒸发量是影响灌区地下水的主要因素. 目前大多地下水数值模型参数间存在耦合关系，只改变单一参数的敏感度可能缺乏代表性和全面性. 模拟研究多参数污染物迁移情况可有效确定关键影响因素，由此提出的正交试验法可有效筛选出全面、均匀、具有代表性的试验组分，以少量模拟迭代得到最优参数，实现复杂模型的优化迭代求解. 正交试验法在实际应用中具有一定可行性，是对传统敏感性分析方法的补充和完善.
基于此为研究污染物迁移的影响因素，本文以甲苯和三氯乙烯为模拟因子，利用GMS软件，结合不同水文地质条件和水动力条件的情景设置，模拟不同情景下污染物迁移过程，分别利用局部分析法和正交试验法评价参数敏感性大小，定量分析各参数变化对污染形态、范围和位置的影响，确定关键影响因素，对分析管理受污染含水层，地下水风险评估及水资源合理利用等有借鉴意义.
-
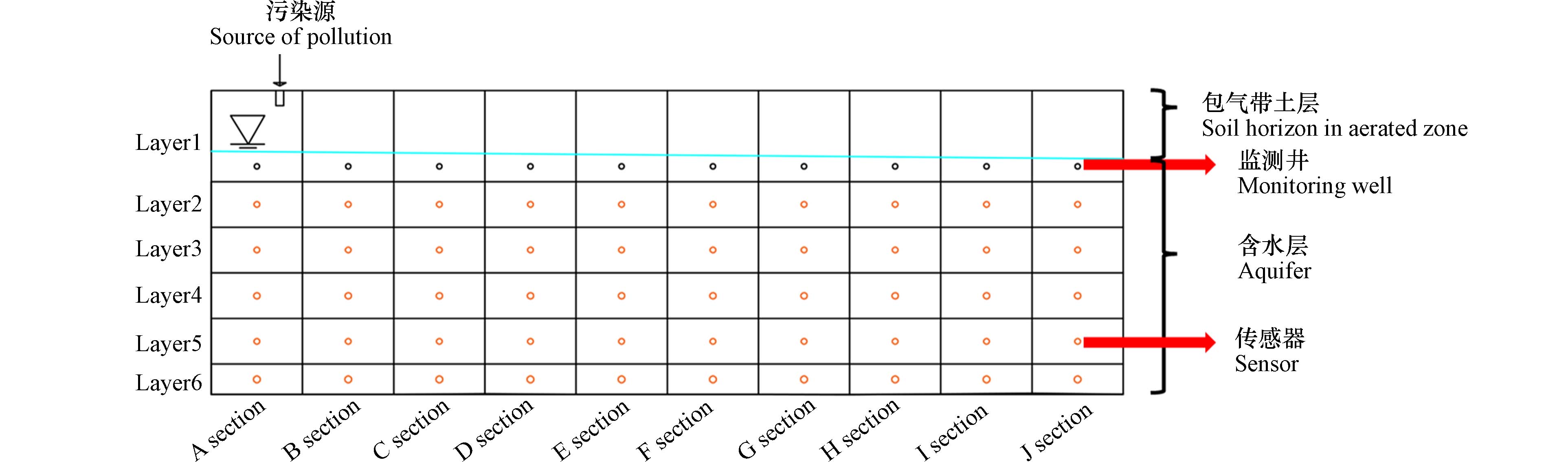
为探究复合有机污染物迁移的关键影响参数和迁移规律，构建大型地下水试验装置，试验装置尺寸为：长5.8 m×宽2.8 m×高2.0 m，装置内设有70个φ60的土壤参数监测口及水样取样口，装置左右两侧安装格栅，利用自动供排水系统控制两侧水头；内部装填200 cm试验土壤，土壤采集于北京市顺义区白庙村实验场地表层0—30 cm处. 分别在装置表土以下20、50、80、110、140、170、200 cm处埋设传感器，传感器之间间隔为0.6 m，监测土壤水分、温度、水势等土壤理化参数. 装填土壤后静置1月使其自然沉降，形成稳定土体结构，设置上下游水头分别为1.6 m、1.55 m，形成5 cm水头差的地下水环境. 大型地下水试验装置结构图及实物图如图1所示.
以甲苯和三氯乙烯混合溶液为污染物，人为投加污染物模拟泄露污染，在装置内部埋设一根2.5 m滴灌管，用三通阀门与污染源连通，污染物为10 mg·L−1的甲苯和三氯乙烯复合溶液，利用蠕动泵泵入土壤中，泄露时间为90 d. 水样取样频率为每5天取样监测，在运行90 d后每15天取样检测，监测甲苯和三氯乙烯在含水层中的浓度变化.
-
在水文地质概念模型和基础渗流方程建立的基础上，结合大型地下水试验装置边界条件、补给率、地下水变化情况、根据室内实验获取的各水文地质参数等水文地质特征，综合分析，将大型地下水试验装置概化为均质各向同性地下水流系统. 地下水流数学模型采用如下1式表示[25]：
式中：D为地下水渗流区域；kxx，kyy，kzz为在x，y和z方向上的渗透系数分量，L·T−1；H为水位标高，L；W为单位体积流量，即源汇项，L3·T−1；μs为蓄水率，L−1；H（x,y,z,t）t=0初始时刻水头函数；H0（x,y,z）为初始地下水水头，L；H（x,y,z,t）为第一类边界已知地下水水头函数；
$ {\Gamma _1} $ 为模型的第一类边界条件；$ {\Gamma _2} $ 为模型的第二类边界条件；n为边界$ {\mathrm{\Gamma }}_{2} $ 上的外法线方向；q（x,y,z）为第二类边界的已知流量函数，L3·T−1.地下水流模型中将试验装置长5.8 m×宽2.8 m×高2.0 m等比例概化；设置边界条件，其中上下游水头设为定水头，水头值分别为1.60 m、1.55 m；装置侧边为密封钢架结构，设为隔水边界. 在模型概化中将传感器设置在每层的中心，将包气带与含水层以下0.2 m设置为1层，故将土体概化成Layer1-Layer6共6层均质各向同性含水层结构；底板高程分别为0、0.2、0.5、0.8、1.1、1.4 m，顶板高程分别为：0.2、0.5、0.8、1.1、1.4、2 m. 同时将传感器所在列划分为一个断面，共A-J10个断面，地层划分如图2所示. 模型中含水率由传感器测得，渗透系数、弥散度、土壤容重均由室内实验获取，水平横向弥散与纵向色散弥散之比（TRPT）、垂直横向弥散与纵向弥散之比（TRVT）为模型默认值，利用GMS中3Dgrid模块对研究区离散化. 采用矩形网格剖分研究区，网格间距为10 cm×10 cm，共剖分为
32480 个网格，在layer1中传感器位置设置10个观测井，模拟地下水流过程，对比监测井水位构建地下水流模型. -
控制方程：地下水溶质运移模型考虑将地下水弥散，其次将坐标轴系统运用到水流方向，水流的主方向和坐标轴重合，溶液密度视为恒定项，存在局部平衡吸附和一级不可逆动力学反应[26 − 27]，对于溶解相和吸附相，两者的速率在过程中相等. 在此前提下，溶质运移的三维水动力弥散方程的数学模型如下[25]：
式中：C为地下水中组分的溶解相浓度，M·L−3；
$\theta $ 为地层介质中的孔隙度，无量纲；xi为沿直角坐标系轴向的距离，L；Dij为水动力弥散系数张量，L2·T−1；vi为孔隙水平均实际流速，L·T−1；qs为单位体积含水层流量，代表源和汇，L3·T−1；Cs为源或汇水流中组分的浓度，M·L−3；Rn为化学反应项，M·L−3·T−1.初始条件：投入污染物位置作为本次模拟的污染源，污染物迁移对周边地下水环境产生持续影响，将污染源视为补给浓度边界，补给浓度值为C0，不产生污染物迁移的位置补给浓度为0. 具体表述为：
溶质运移模型中污染物吸附系数及吸附特性均由静态实验获取. 化学反应（Chemical Reaction Package）中甲苯吸附类型为Linear ，吸附平衡常数为60.50 L·kg−1；三氯乙烯吸附类型为Freundlich，吸附平衡常数为49.60 L·kg−1，模拟污染物在试验装置中迁移过程.
-
本研究敏感性分析采用局部分析法中的因子变化法[13]和正交试验法[28]，对渗透系数、弥散度和吸附系数进行单因素及多因素敏感性分析. 局部敏感性分析指数如公式4所示. 正交试验法中以均方根误差（RMSE）为目标函数来描述模型对参数的敏感程度如公式5所示.
式中：L为敏感性指数，无量纲；n为参数水平值个数，即每种参数模拟次数；cj为对照组特征污染物纵向迁移距离，m；c′ｊ为敏感性分析时每次模拟的纵向迁移距离，m.
-
地下水流模型中模拟大型地下水试验装置内1年的水位变化情况，以运行200 d为模拟期，201—365 d为验证期，对比监测井水位识别验证，试验装置内地下水流为稳定流，相同观测井水位随时间变化程度小，layer1中10个观测井观测值与模拟值呈现线性拟合，R2=0.972，RMSE为0.24 cm，验证数据点落在95%置信区间内，拟合效果较好. 地下水流模型能够良好刻画试验装置内地下水环境，由模型验证结果可知地下水流模型中渗透系数、弥散度、TRPT、TRVT和土壤容重分别为0.23 m·d−1、1.5 m、0.1、0.1和1.38 g·cm−3，可进行复合污染物溶质运移模拟及敏感性分析.
-
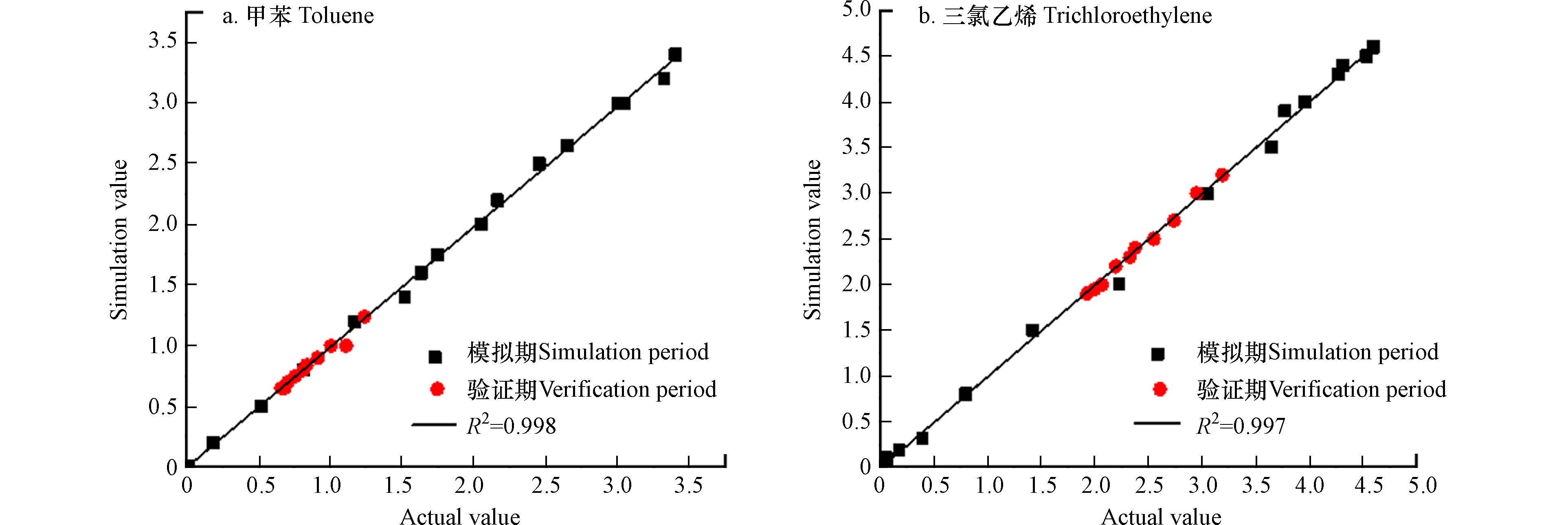
溶质运移模型模拟时长为365 d，应力期和时间步长与取样频率一致，200 d为模拟期，201—365 d为验证期，比较各取样点实测值与模拟值浓度变化，以第三层C断面取样点为例，如图3中甲苯和三氯乙烯实测值和模拟值呈线性相关，决定系数R2分别为0.997、0.998，说明溶质运移模型构建良好，可进一步探究影响污染物迁移关键参数.
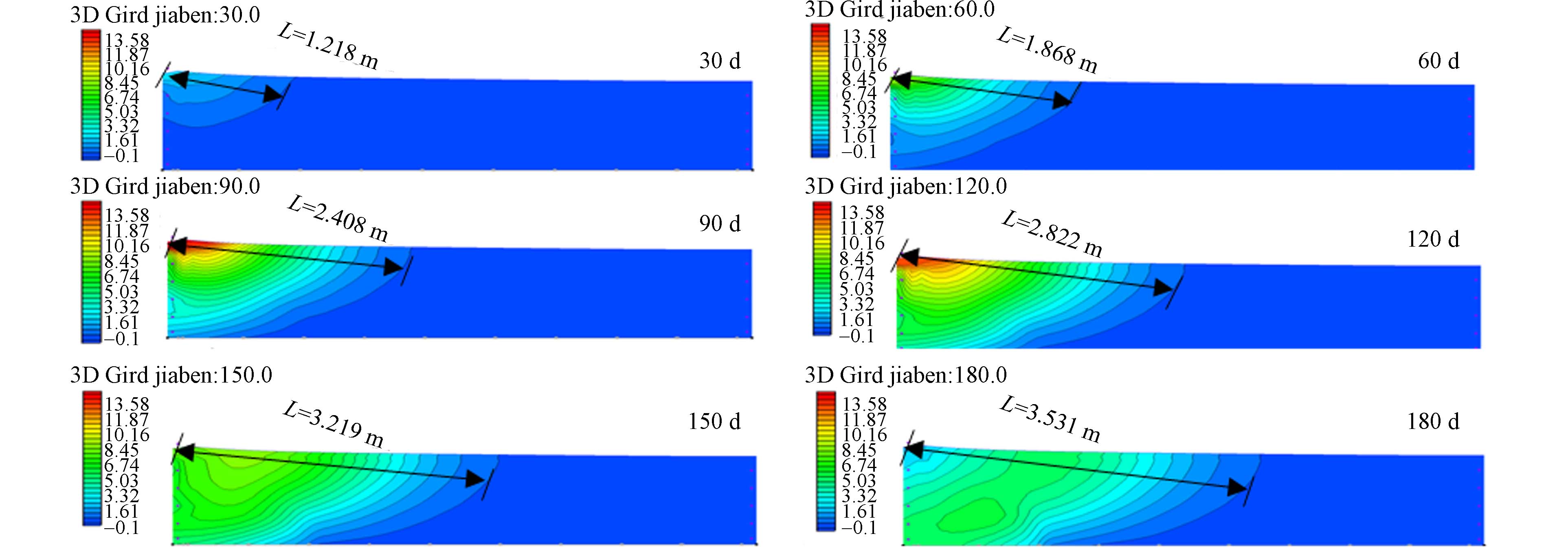
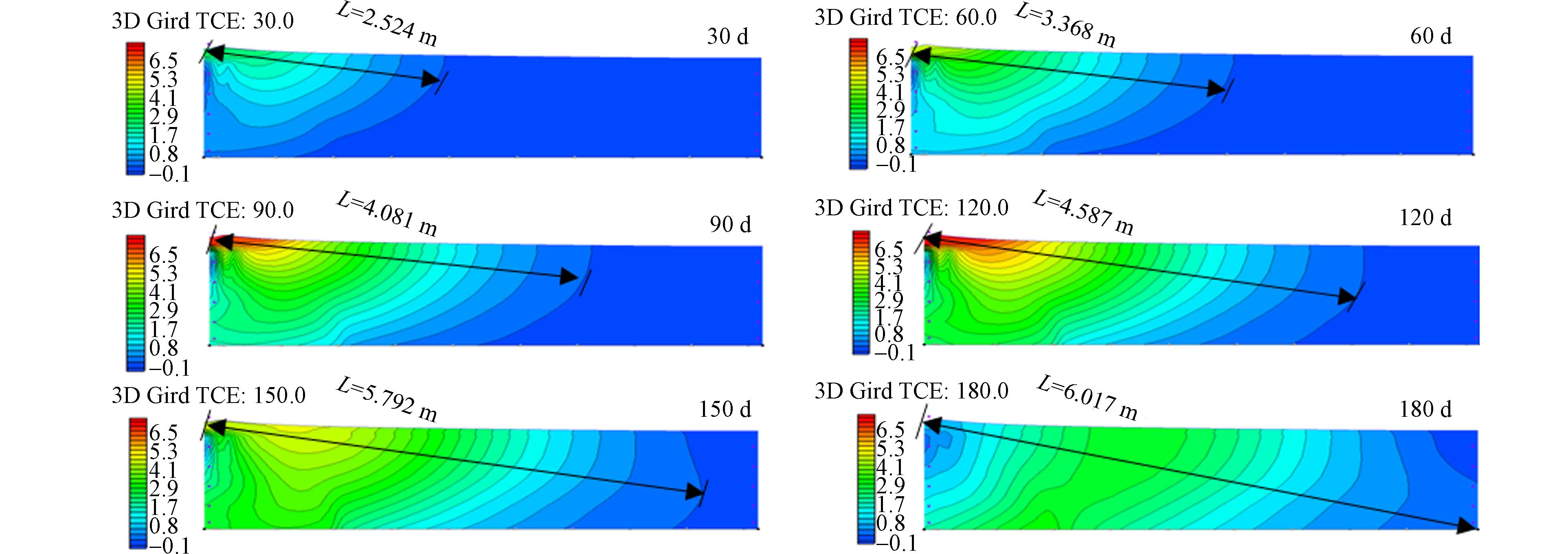
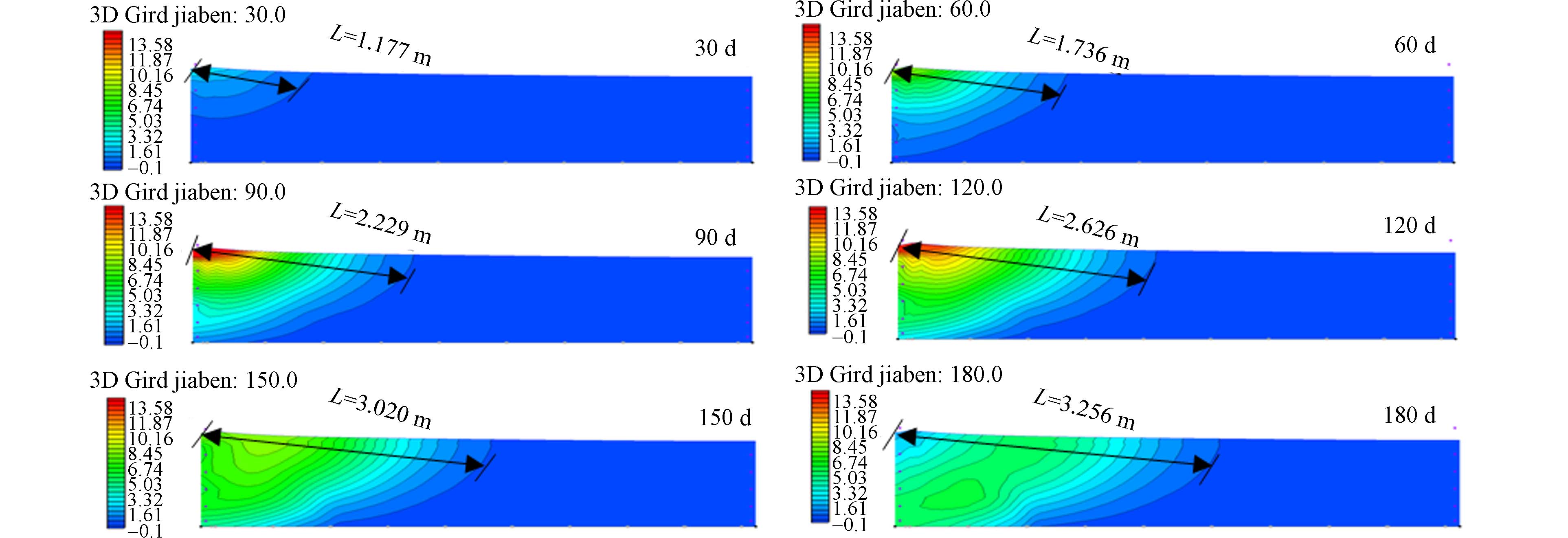
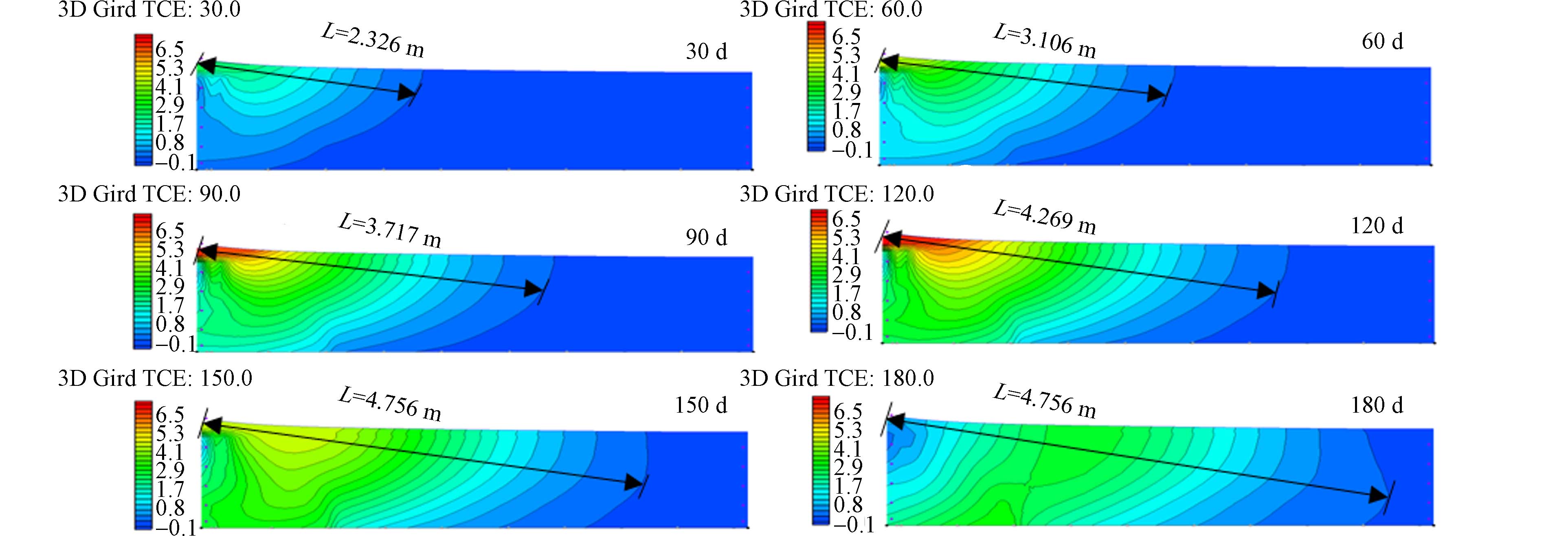
甲苯迁移过程及迁移距离如图4所示，三氯乙烯迁移过程及迁移距离如图5所示. 通过模拟发现甲苯和三氯乙烯在大型地下水试验装置中均发生多维度迁移，在运行180 d时，甲苯迁移的最远距离为3.531 m；三氯乙烯在180 d时已经穿透大型地下水试验装置，其迁移受到大型地下水试验装置尺寸的限制，迁移最远距离为试验装置最远距离6.017 m；装置内污染物浓度呈现先增加后缓慢降低趋势，污染羽范围不断扩大. Ayad等[29]探究了三维槽试验标准砂介质中三氯乙烯羽流的时空分布特征. 结果表明最高浓度出现在源区附近，随着流量的增加，污染物纵向和横向迁移增加，迁移规律与文本类似，说明模拟结果符合污染物迁移的一般规律.
分析认为复合污染受到吸附类型的影响，甲苯符合Linear型吸附，受分配作用影响，吸附作用大，受土壤阻碍作用强，甲苯在含水层中迁移能力较弱. 三氯乙烯符合Freundlich型吸附，受分配作用和表面吸附共同作用，吸附作用小，土壤介质阻碍作用弱，三氯乙烯在含水层中迁移较快，说明含水层中三氯乙烯迁移能力强于甲苯. E1-Farhan等[30]利用土柱实验探究了甲苯和三氯乙烯复合体系下迁移规律，研究发现甲苯受吸附降解作用，多在土柱入口处检出；三氯乙烯不易吸附降解扩散更快，多在出口处检出，因此复合体系下三氯乙烯的迁移能力强于甲苯，该结果与本文实验结果一致，说明污染物迁移能力受吸附类型影响.
-
本文采用局部法中的因子变换法，对渗透系数、弥散度及吸附系数进行敏感性分析，将模型验证后参数值作为对照组，分别将渗透系数、弥散度及吸附系数等参数值上下浮动±10%、±20%四个水平进行模拟. 模拟组分各参数值如表1所示.
以渗透系数减小幅度20%为例，甲苯迁移过程及迁移距离如图6所示，与对照组相比，在迁移30、60、90、120、150、180 d时，迁移距离分别减少了0.041、0.132、0.179 、0.202 、0.199 、0.51 m，相较于对照组基准值变动7.5%；三氯乙烯的迁移距离如图7所示，较对照组减少了0.198、0.262 、0.364 、0.322 、1.036 、0.604 m，迁移180 d三氯乙烯穿透大型地下水试验装置，迁移距离不具有参考意义，剔除该数据，计算得到与对照组基准值相比减小了11.0%.
绘制迁移距离随参数变化如图8（a）、（b）所示可知，变幅为±20%时，渗透系数对甲苯和三氯乙烯的迁移影响最大，迁移距离分别变动了13.5%和14.2%；弥散度对甲苯和三氯乙烯影响均为8.2%. 吸附系数对甲苯和三氯乙烯迁移影响分别为8.2%和0.8%，甲苯与三氯乙烯迁移距离相差一个数量级. 利用敏感性指数计算公式计算各参数敏感度，影响甲苯迁移的渗透系数、弥散度、吸附系数敏感度分别为0.05、0.03、0.03；影响三氯乙烯迁移的敏感度分别为0.05、0.03、0.005. 由此得到甲苯迁移的敏感参数：渗透系数>弥散度=吸附系数. 三氯乙烯迁移的敏感参数：渗透系数>弥散度>吸附系数. 还发现在±20%范围内浮动，特征污染物迁移距离与渗透系数和弥散度呈线性正相关，与各自吸附系数呈线性负相关.
-
本文正交试验中将参数增减±20%，依据三因素三水平设计模拟9种参数组合下污染物的迁移情况，与对照组极差作为敏感性指标，分别记为指标1和指标2，如表2所示.
以表2中渗透系数为例，找出因素为渗透系数降幅为20%的所有组分（试验组分1、2、3）. 甲苯模拟迁移距离分别为2.623、2.624、2.625 m，指标为0.199、0.198、0.197，计算指标平均值得到降幅为20%时，渗透系数的敏感度为0.198；三氯乙烯迁移距离分别4.151、4.192、4.200 m，指标分别为0.436、0.395、0.387，得到渗透系数的敏感度为0.406，以此计算各组分敏感性指标，利用均方根误差得到各因素敏感度如表3所示.
利用正交试验法探究各参数变化对甲苯和三氯乙烯迁移影响，绘制各参数敏感度对比图8（c）、（d）所示，污染物迁移的敏感性指标：渗透系数>弥散度>吸附系数，与局部敏感性分析中甲苯敏感度：渗透系数>弥散度=吸附系数不同，说明参数间相互影响关系改变敏感度大小. 分析认为污染物迁移过程中，渗透系数通过孔隙-水速度直接影响含水层中污染物空间和时间上的位移变化，弥散度和吸附系数通过弥散作用及吸附作用间接影响污染物迁移过程[31]，导致了渗透系数对迁移的影响更强. 同时受到吸附类型的影响，吸附系数越大，迁移能力越弱，敏感性越强，甲苯的吸附作用远大于三氯乙烯导致了甲苯的敏感度远大于三氯乙烯. 正交试验法中敏感度整体变大，说明该方法对参数变化引起的迁移变化响应更灵敏，广泛适用于处理高维输入变量的水文环境问题.
GMS因建模方法灵活，兼容性好的优点，广泛应用于地下水数值模拟领域，本文基于GMS模拟，实现了大型地下水试验装置复合有机污染物迁移过程模拟，利用参数敏感性分析识别敏感参数，可有效提高参数率定验证效率，实现了以少次数模拟迭代寻求关键影响参数，有助于复杂模型的优化迭代求解，降低模型模拟结果不确定性问题，对开展实际场地污染物迁移模拟研究及关键参数确定有借鉴意义，为防治环境退化和地下水修复治理提供了重要的理论基础.
-
（1）利用GMS模拟试验装置内甲苯和三氯乙烯迁移过程，发现污染物浓度在三维空间内均呈现先增大后减小趋势，污染羽范围不断扩散；对比装置内污染物浓度模拟值和观测值，两者呈良好线性相关，模拟结果表明大型地下水试验装置污染物迁移模拟有效规避了边壁效应及模拟误差导致的模拟不精确问题，使污染物迁移更接近真实场地迁移过程；污染物迁移180 d时甲苯迁移距离为3.531 m，三氯乙烯完全穿透试验装置，说明三氯乙烯迁移能力强于甲苯.
（2）局部分析法中影响甲苯迁移的敏感度大小为：渗透系数>弥散度=吸附系数，影响三氯乙烯迁移的敏感度大小为：渗透系数>弥散度>吸附系数；污染物迁移距离与渗透系数和弥散度呈线性正相关，与吸附系数呈线性负相关. 正交试验法得到影响甲苯和三氯乙烯迁移的敏感度排序相同，均为渗透系数>弥散度>吸附系数，说明与单一参数相比，参数之间存在相互影响关系；正交试验法中敏感度整体大于局部分析法，表明了正交试验法对参数变化引起的不确定性识别能力更强.
（3）本文利用GMS构建溶质运移模型，进行敏感性分析，确定了研究区溶质运移的主要影响因素，实现了污染物迁移过程的精细刻画，为地下水污染风险评估和科学管理提供了决策参考依据；正交试验法实现了用部分试验代替全部试验，有效降低参数维度减小运算成本，适用于识别复杂多过程模型的多参数不确定性来源，是传统敏感性分析方法的补充和完善，可广泛用于处理高维输入变量的水文环境问题.
基于大型地下水试验装置的复合有机污染物迁移性能关键影响参数研究
Study on the key factors affecting the migration of complex organic pollutants based on a large-scale groundwater test device
-
摘要: 含水层中的复合污染物迁移过程主要受水文地质条件和水动力条件影响，为探究复合污染物迁移的影响因素，基于建设的大型地下水试验模拟装置，以甲苯和三氯乙烯为特征污染物，利用GMS建立了地下水流模型和溶质迁移模型，并设置不同情景，模拟不同水文地质条件和水动力条件影响下复合污染物迁移过程；通过敏感性分析，探究关键因素的影响. 模拟结果表明三氯乙烯迁移能力大于甲苯，模型运行180 d后，甲苯最大迁移距离为3.5 m，而三氯乙烯最大迁移距离超过6.0 m，且甲苯和三氯乙烯迁移距离与渗透系数和弥散度呈线性正相关，与吸附系数呈线性负相关，即迁移距离随渗透系数和弥散度的增大而增大，随吸附系数的增大而减小. 敏感性分析结果表明复合污染物迁移程度的关键影响因素为：渗透系数>弥散度>吸附系数.Abstract: The migration process of complex pollutants in aquifers is mainly affected by hydrogeological and hydrodynamic conditions. In order to explore the factors affecting the migration of complex pollutants, toluene and trichloroethylene were used as characteristic pollutants. Groundwater modeling system (GMS) was adopted to establish the groundwater flow model and solute migration model based on large-scale groundwater test device under different scenarios. Then, the migration process of complex pollutants under the influence of different hydrogeological and hydrodynamic conditions was simulated. Meanwhile, the influence of key factors was explored through sensitivity analysis. The simulation results showed that the migration capacity of trichloroethylene was greater than that of toluene. The maximum migration distance of toluene was 3.5 m, while the maximum migration distance of trichloroethylene was more than 6.0 m after 180 days. The migration distances of toluene and trichloroethylene were linearly positively correlated with the permeability and dispersion coefficients, and linearly negatively correlated with the adsorption coefficient, indicating that the migration distances increase with the increase of permeability and dispersion coefficients, and decrease with the increase of adsorption coefficient. The results of sensitivity analysis showed that the most key factor affecting the migration degree of composite pollutants was permeability coefficient, followed by dispersion and adsorption coefficients.
-
-
图 1 大型地下水试验装置结构图及实物图
Figure 1. Structure diagram and physical diagram of large-scale groundwater test device
图 3 甲苯和三氯乙烯运移模型模拟及验证
Figure 3. Simulation and verification of toluene and trichloroethylene transport models
图 6 渗透系数下调 20%后甲苯迁移过程图
Figure 6. Migration process of toluene by 20% cut of permeability coefficient
图 7 渗透系数下调20%后三氯乙烯迁移过程图
Figure 7. Migration process of trichloroethylene by 20% cut of permeability coefficient
图 8 特征污染物的迁移距离随参数变幅变化图（a、b）及敏感度随敏感参数变化图（c、d）
Figure 8. The migration distance of characteristic pollutants with the change of parameters （a, b） and the sensitivity with the change of sensitive parameters （c, d）
表 1 参数水平值
Table 1. Level values of the parameters
参数
Parameter水平1
Level 1水平2
Level 2对照组
Control group水平3
Level 3水平4
Level 4−20% −10% 0 10% 20% 渗透系数/（m·d−1）
Permeability0.18 0.21 0.23 0.25 0.28 弥散度/m
Dispersity1.20 1.35 1.50 1.65 1.80 吸附系数甲苯/（L·kg−1）
Adsorption48.40 54.45 60.50 66.55 72.60 吸附系数三氯乙烯n /（L·kg−1）
Adsorptio39.68 44.64 49.60 54.56 59.52 
下载: 导出CSV
表 2 正交试验方案下参数组合情况及指标值
Table 2. Parameter combination and index values under orthogonal test scheme
试验组分
Constituent test渗透系数/
（m·d−1）
Permeability弥散度/m
DispersityKd甲苯/
（L·kg−1）
AdsorptionKf三氯乙烯/
（L·kg−1）
Adsorption甲苯迁移距离/m
Migration
distance指标1
Indicator1三氯乙烯
迁移距离/m
Migration distance指标2
Indicator21 0.18 1.20 48.40 39.70 2.623 0.199 4.151 0.436 2 0.18 1.50 60.50 49.60 2.624 0.198 4.192 0.395 3 0.18 1.80 72.60 59.50 2.625 0.197 4.200 0.387 4 0.23 1.20 60.50 49.60 2.733 0.089 4.289 0.298 5 0.23 1.50 72.60 59.50 2.733 0.089 4.434 0.153 6 0.23 1.80 48.40 39.70 3.109 0.287 4.617 0.030 7 0.28 1.20 72.60 59.50 2.987 0.165 4.878 0.291 8 0.28 1.50 48.40 39.70 3.219 0.397 4.955 0.368 9 0.28 1.80 60.50 49.60 3.231 0.409 4.960 0.373
下载: 导出CSV
表 3 影响因素敏感度分析
Table 3. Sensitivity analysis of influencing factors
水平/因素
Level/Factor甲苯
Methylbenzene三氯乙烯
Trichloroethylene渗透系数/（m·d−1）Permeability 弥散度/m Dispersity 吸附系数/（L·kg−1）
Adsorption渗透系数/（m·d−1）Permeability 弥散度/m Dispersity 吸附系数/（L·kg−1）
Adsorption−20% 0.198 0.151 0.294 0.406 0.342 0.278 0% 0.155 0.228 0.232 0.163 0.354 0.355 20% 0.324 0.298 0.15 0.344 0.263 0.277 均方根误差
Root mean square error0.072 0.060 0.059 0.103 0.040 0.037 因素敏感性大小
Factor sensitivity渗透系数>弥散度>吸附系数 渗透系数>弥散度>吸附系数
下载: 导出CSV
-
[1] 周美春, 李加鹏, 周杜牧, 等. 复杂有机污染场地地下水风险管控工程效果评估研究——以常州市某污染场地为例[J]. 环境保护科学, 2023, 1(7): 1-10. ZHOU M C, LI J P, ZHOU D M, et al. Effect evaluation of groundwater risk control project in complex organic contaminated site: A case study of a contaminated site in Changzhou[J]. Science of Environmental Protection, 2023, 1(7): 1-10.
[2] LUEDERS T. The ecology of anaerobic degraders of BTEX hydrocarbons in aquifers[J]. FEMS Microbiology Ecology, 2017, 93(1): fiw220. doi: 10.1093/femsec/fiw220 [3] 李笑诺, 陈卫平, 吕斯丹. 国内外污染场地风险管控技术体系与模式研究进展[J]. 土壤学报, 2022, 59(1): 38-53. LI X N, CHEN W P, LÜ S D. Advancement in researches on technical systems and modes for risk management and control of contaminated sites at home and aborad[J]. Acta Pedologica Sinica, 2022, 59(1): 38-53 (in Chinese).
[4] VAN L M H, PROKOP G, RABL-BERGER S, et al. Progress in the management of contaminated sites in Europe[R]. Italy: Joint Research Center of the European Commission, 2014: 3-5. [5] POWERS S E, HUNT C S, HEERMANN S E, et al. The transport and fate of ethanol and BTEX in groundwater contaminated by gasohol[J]. Critical Reviews in Environmental Science and Technology, 2001, 31(1): 79-123. doi: 10.1080/20016491089181 [6] LI Y, WEI M L, LIU L, et al. Adsorption of toluene on various natural soils: Influences of soil properties, mechanisms, and model[J]. Science of the Total Environment, 2020, 740: 140104. doi: 10.1016/j.scitotenv.2020.140104 [7] AKYOL N H, YOLCUBAL I, YÜKSEL D I. Sorption and transport of trichloroethylene in caliche soil[J]. Chemosphere, 2011, 82(6): 809-816. doi: 10.1016/j.chemosphere.2010.11.029 [8] LEE S G, LEE S, CHOI J W. Nonlinear sorption of organic contaminant during two-dimensional transport in saturated sand[J]. Water, 2021, 13(11): 1557. doi: 10.3390/w13111557 [9] 郭晓东, 田辉, 张梅桂, 等. 我国地下水数值模拟软件应用进展[J]. 地下水, 2010, 32(4): 5-7. doi: 10.3969/j.issn.1004-1184.2010.04.002 GUO X D, TIAN H, ZHANG M G, et al. Visual MODFLOW; GMS; FEFLOW application development of groundwater value simulation software in our country[J]. Ground Water, 2010, 32(4): 5-7 (in Chinese). doi: 10.3969/j.issn.1004-1184.2010.04.002
[10] GUO S S, WU H, TIAN Y Q, et al. Migration and fate of characteristic pollutants migration from an abandoned tannery in soil and groundwater by experiment and numerical simulation[J]. Chemosphere, 2021, 271: 129552. doi: 10.1016/j.chemosphere.2021.129552 [11] ZHAO X N, WANG D Q, XU H L, et al. Simulation and prediction of groundwater pollution based on GMS: A case study in Beijing, China[J]. IOP Conference Series:Earth and Environmental Science, 2021, 826(1): 012014. doi: 10.1088/1755-1315/826/1/012014 [12] 刘玲, 陈坚, 牛浩博, 等. 基于FEFLOW的三维土壤-地下水耦合铬污染数值模拟研究[J]. 水文地质工程地质, 2022, 49(1): 164-174. LIU L, CHEN J, NIU H B, et al. Numerical simulation of three-dimensional soil-groundwater coupled chromium contamination based on FEFLOW[J]. Hydrogeology & Engineering Geology, 2022, 49(1): 164-174 (in Chinese).
[13] 束龙仓, 王茂枚, 刘瑞国, 等. 地下水数值模拟中的参数灵敏度分析[J]. 河海大学学报(自然科学版), 2007, 35(5): 491-495. SHU L C, WANG M M, LIU R G, et al. Sensitivity analysis of parameters in numerical simulation of groundwater[J]. Journal of Hohai University (Natural Sciences), 2007, 35(5): 491-495 (in Chinese).
[14] YASEMI M, JOLICOEUR M. Modelling cell metabolism: A review on constraint-based steady-state and kinetic approaches[J]. Processes, 2021, 9(2): 322. doi: 10.3390/pr9020322 [15] 吴吉春, 陆乐. 地下水模拟不确定性分析[J]. 南京大学学报(自然科学版), 2011, 47(3): 227-234. WU J C, LU L. Uncertainty analysis for groundwater modeling[J]. Journal of Nanjing University (Natural Sciences), 2011, 47(3): 227-234 (in Chinese).
[16] STEWART I T, LOAGUE K. A type transfer function approach for regional-scale pesticide leaching assessments[J]. Journal of Environmental Quality, 1999, 28(2): 378-387. [17] CHEN M, IZADY A, ABDALLA O A, et al. A surrogate-based sensitivity quantification and Bayesian inversion of a regional groundwater flow model[J]. Journal of Hydrology, 2018, 557: 826-837. doi: 10.1016/j.jhydrol.2017.12.071 [18] ANDERSON M P, WOESSNER W W, HUNT R J. Applied groundwater modeling: simulation of flow and advective transport[M]. London: Academic press, 2015. [19] DAI H, CHEN X Y, YE M, et al. A geostatistics-informed hierarchical sensitivity analysis method for complex groundwater flow and transport modeling[J]. Water Resources Research, 2017, 53(5): 4327-4343. doi: 10.1002/2016WR019756 [20] ABDELAZIZ R, MERKEL B J. Sensitivity analysis of transport modeling in a fractured gneiss aquifer[J]. Journal of African Earth Sciences, 2015, 103: 121-127. doi: 10.1016/j.jafrearsci.2014.12.003 [21] SHI X Q, YE M, CURTIS G P, et al. Assessment of parametric uncertainty for groundwater reactive transport modeling[J]. Water Resources Research, 2014, 50(5): 4416-4439. doi: 10.1002/2013WR013755 [22] WANG Y, WEI W X, HAN H L, et al. Groundwater migration modeling and parameter sensitivity analysis on contaminated site[J]. Advanced Materials Research, 2014, 878: 775-781. doi: 10.4028/www.scientific.net/AMR.878.775 [23] SONG X M, ZHANG J Y, ZHAN C S, et al. Global sensitivity analysis in hydrological modeling: Review of concepts, methods, theoretical framework, and applications[J]. Journal of Hydrology, 2015, 523: 739-757. doi: 10.1016/j.jhydrol.2015.02.013 [24] 张冠儒, 魏晓妹. 基于变化环境的地下水动态敏感性分析方法研究[J]. 西北农林科技大学学报(自然科学版), 2011, 39(2): 223-228. ZHANG G R, WEI X M. Methods study on sensitivity analysis of groundwater dynamics based on the changing environment[J]. Journal of Northwest A & F University (Natural Science Edition), 2011, 39(2): 223-228 (in Chinese).
[25] APPELO C A J, POSTMA D. Geochemistry, Groundwater and Pollution[M]. Rotterdam: CRC Press, 2004. [26] SCHAFFER M, LICHA T. A framework for assessing the retardation of organic molecules in groundwater: Implications of the species distribution for the sorption-influenced transport[J]. Science of the Total Environment, 2015, 524/525: 187-194. doi: 10.1016/j.scitotenv.2015.04.006 [27] DELLE SITE A. Factors affecting sorption of organic compounds in natural sorbent/water systems and sorption coefficients for selected pollutants. A review[J]. Journal of Physical and Chemical Reference Data, 2001, 30(1): 187-439. doi: 10.1063/1.1347984 [28] 苗胜军, 李长洪, 文俊, 等. 基于正交试验设计的滑带土参数敏感性分析[J]. 中国矿业, 2007, 16(9): 76-79. doi: 10.3969/j.issn.1004-4051.2007.09.024 MIAO S J, LI C H, WEN J, et al. Parameter sensitivity analysis of slip zone based on orthogonal experiment[J]. China Mining Magazine, 2007, 16(9): 76-79 (in Chinese). doi: 10.3969/j.issn.1004-4051.2007.09.024
[29] FAISAL A A H, KUBBA F A, MADHLOOM H M. Modeling of trichloroethylene migration in three-dimensional saturated sandy soil[J]. Arabian Journal for Science and Engineering, 2014, 39(11): 7763-7769. doi: 10.1007/s13369-014-1326-x [30] EL-FARHAN Y H, SCOW K M, DE JONGE L W, et al. Coupling transport and biodegradation of toluene and trichloroethylene in unsaturated soils[J]. Water Resources Research, 1998, 34(3): 437-445. doi: 10.1029/97WR03466 [31] GATEL L, LAUVERNET C, CARLUER N, et al. Global evaluation and sensitivity analysis of a physically based flow and reactive transport model on a laboratory experiment[J]. Environmental Modelling & Software, 2019, 113: 73-83. -
点击查看大图
计量
- 文章访问数: 1253
- HTML全文浏览数: 1253
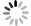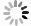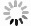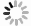
- PDF下载数: 22
- 施引文献: 0
