-
全/多氟烷基化合物（PFASs），是分子中包含至少一个完全氟化的甲基或亚甲基碳原子（不连接任何氢、氯、溴、碘原子）的化学物质[1]. PFASs具有很强的化学稳定性、表面活性及优良的热稳定性[2 − 5]，应用广泛[6 − 7]. PFASs种类达1.2万种以上[8]，已在多种环境介质中被检出[9 − 12]，可诱导人体产生心脏代谢疾病[13]、内分泌紊乱[14]和肾功能损伤[15]等问题. 因此，需加强对PFASs类化学品的管理.
正辛醇-水分配系数（KOW）是化学品暴露和危害性评价的关键参数[16 − 17]. 由于多数PFASs易在界面聚集[18]、标准品缺乏和分析检测困难等问题，实验获取PFASs的KOW数据非常有限. 有必要发展PFASs的KOW预测方法. 前人针对PFASs，构建了定量构效关系（QSAR）模型用于预测KOW[19 − 20]. 然而，构建QSAR模型所用的数据集都较小，导致模型的预测可靠性低. 发展基于分子模拟手段预测PFASs的KOW方法，是解决PFASs的KOW缺失的一个重要路径.
分子模拟方法，可通过计算PFASs从水相转移到正辛醇相的自由能变（∆GOW），并通过热力学关系式预测其KOW. 基于显式溶剂化模型的分子力学或量子力学方法计算∆GOW[21]，对算力的要求高. 隐式溶剂化模型，将溶剂作为均匀连续介质来描述，具有较快的计算速度[22 − 24]. 预测KOW的不同方法的原理及优缺点见表1. 真实溶剂类导体屏蔽（COSMO-RS）模型[25]，被成功用于预测3种氟调聚醇的KOW. 相比于COSMO-RS，基于溶质电子密度的溶剂化模型（SMD）[26]明确定义了溶剂效应的非极性部分，可以更好地描述体系的非极性作用. Li等[27]基于SMD模型发展了多氯联苯KOW的预测方法，具有较高的准确性，预测和实测lgKOW的决定系数（R2）为0.905，均方根误差（RMSE）为0.249. 然而，目前尚没有针对PFASs建立基于SMD模型的KOW预测方法.
本研究基于搜集的19个PFASs的lgKOW实测数据，通过SMD模型描述溶剂化效应，从哈特里-福克（HF）自洽场和密度泛函理论（DFT）与不同基组的组合中筛选适合方法，考察了其预测PFASs的lgKOW的准确性，为获取PFASs的lgKOW值提供了一种可靠的方法.
-
从文献和数据库中收集了19种PFASs实测值（表2），用于筛选合适的计算方法，涉及全氟羧酸、全氟磺酸、全氟烷基磺酰胺和氟调聚醇等. 全氟羧酸和全氟磺酸的酸解离系数（pKa）小于4[28]，主要以阴离子形式存在于水中[29]. 所计算的全氟羧酸和全氟磺酸，均为阴离子结构，其余PFASs为中性分子结构.
所有计算在Gaussian 09软件（Revision D.01）[35]中进行. 通过GaussView软件（Ver. 6）[36]绘制19个PFASs的初始结构. 参考前人的研究[26 − 27]，选择适于SMD模型的4种理论方法：HF[37], B3LYP[38], M05-2X[39]和M06-2X[40]以及5种基组：6-31G（d）[41], 6-31G（d,p）[42], 6-31+G（d,p）[43], cc-pVTZ[44]和MIDI!6D[45]. 将4种理论方法分别与5种基组组合，通过SMD模型模拟正辛醇和水相，优化PFASs在两相中的几何结构. 基于优化后的结构，保持理论方法不变，分别与上述5种基组组合，计算PFASs在两相中的自由能（G）[46]. PFASs的∆GOW由正辛醇和水相中的G之差得出，根据∆GOW （J·mol−1）计算lgKOW值：
式中，R为摩尔气体常数（8.314 J·mol−1·K−1），T为温度（本研究T = 298.15 K）. 根据SMD的原理，G由3部分组成[26]：
式中，GENP为静电能（J·mol−1），GCDS为非静电能（J·mol−1），∆GCONC为气相与液相标准态浓度变化常数项（7.908×103 J·mol−1）.
由此，SMD计算的∆GOW，可以由下式表示：
式中，
${{G}}_{\text{ENP}}^{\text{O}}$ 为溶质在正辛醇相中的静电能（J·mol−1），${{G}}_{\text{ENP}}^{\text{W}}$ 为溶质在水相中的静电能（J·mol−1），${{G}}_{\text{CDS}}^{\text{O}}$ 为溶质在正辛醇相中的非静电能（J·mol−1），${{G}}_{\text{CDS}}^{\text{W}}$ 为溶质在水相中的非静电能（J·mol−1）.${{\Delta }{G}}_{\text{ENP}}^{\text{OW}}$ 为溶质在正辛醇和水相中的静电能之差（J·mol−1），${{\Delta }{G}}_{\text{CDS}}^{\text{OW}}$ 为溶质在正辛醇和水相中的非静电能之差（J·mol−1）. -
对lgKOW预测值与实测值进行线性回归分析，采用t检验对回归系数的显著性进行检验. 采用相关系数（r），显著性水平（P）和RMSE评价预测和实测值间的相关性及差异. r值越高，P值越低，RMSE值越低，方法的预测准确性越高.
其中，xi和yi分别为第i个化合物的实测值和预测值，
$\stackrel{\mathrm{-}}{{x}}$ 为所有实测值的平均值，$\stackrel{\mathrm{-}}{y}$ 为所有预测值的平均值，n为样本容量. -
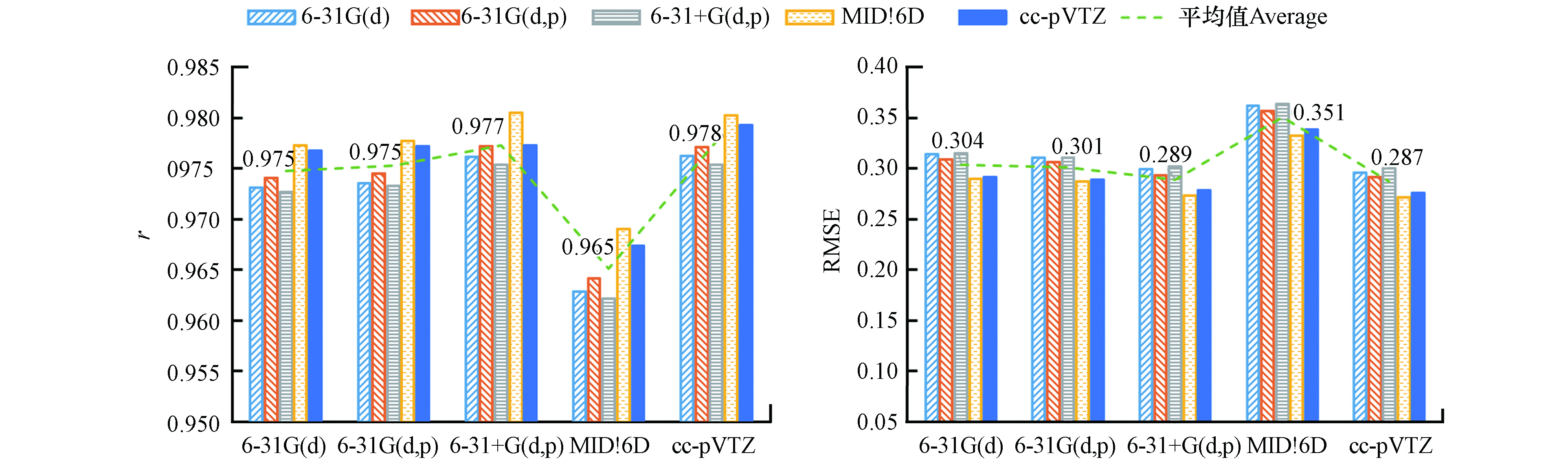
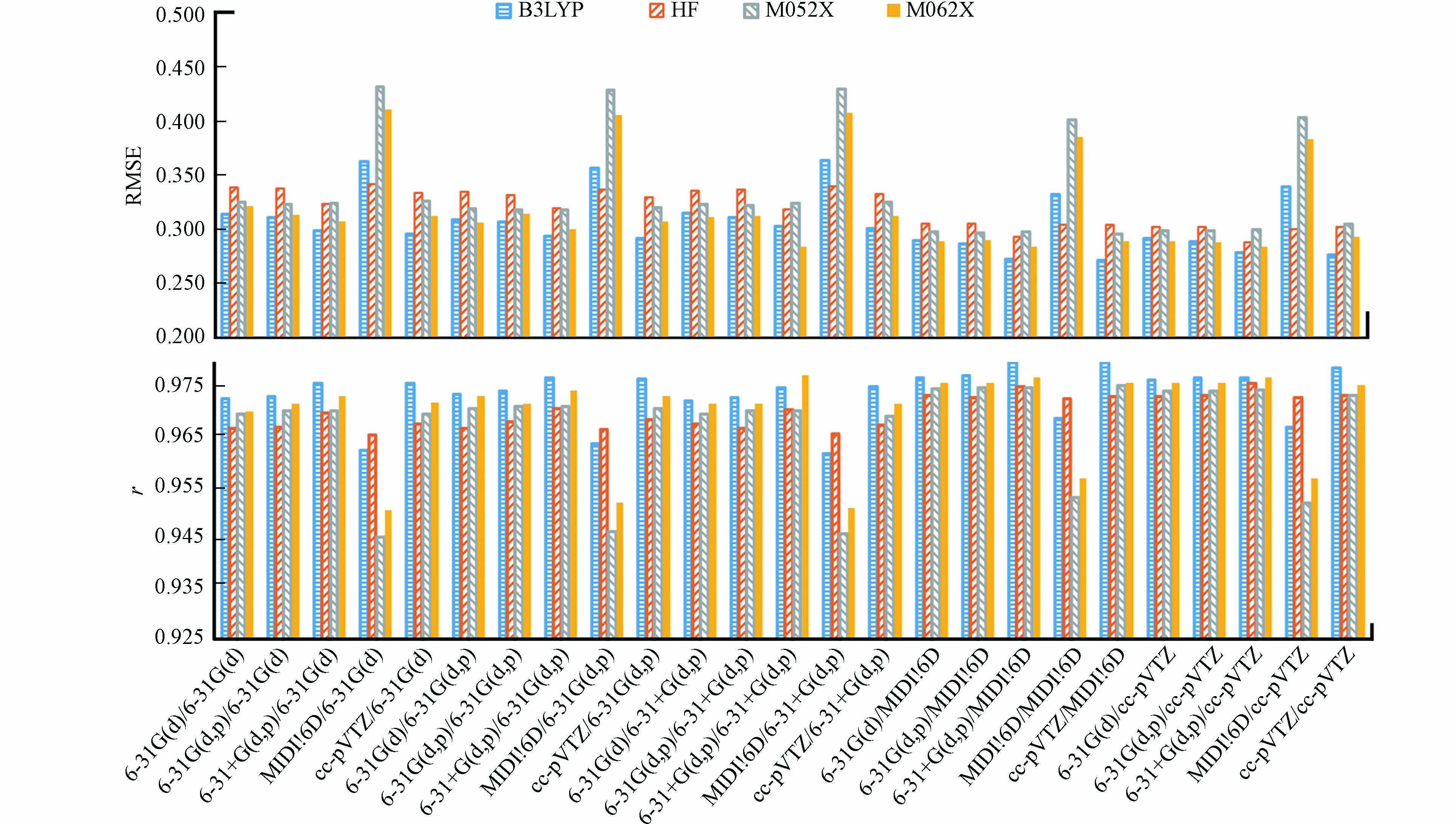
如图1所示，使用B3LYP泛函得到的lgKOW预测值，总体上与实测值有较高的r和较低的RMSE，效果较好；M062X泛函效果略差，但优于M052X泛函的预测结果. 在采用MIDI!6D基组进行几何结构优化的情况下，HF方法取得了较优的预测结果，但总体上HF方法的预测效果最差.
HF方法仅考虑了电子之间的时间平均相互作用，没有考虑电子间的瞬时相关引起的电子相关能[37]，这可能是其效果最差的原因. B3LYP、M05-2X和M06-2X属于密度泛函，考虑了电子相关能[47 − 48]，因此预测结果更优. M05-2X和M06-2X作为高度参数化的杂化泛函，能准确描述非共价相互作用[48]. 与M05-2X泛函相比，M06-2X泛函能较好的获取中程交换相关能[48]，因此其效果更优. B3LYP比M06-2X和M05-2X泛函在对小分子几何优化和振动分析方面表现更好[49]，这可能是B3LYP泛函取得最好结果的原因.
-
如图2所示，优化PFASs几何结构时，使用B3LYP泛函，结合6-31+G（d,p）基组或cc-pVTZ基组的效果较优，这可能是因为它们基组大，优化的结构更准确[37]. 而6-31G（d）, 6-31G（d,p）和MIDI!6D基组相对较小，效果较差.
在能量计算方面，MIDI!6D基组表现最优. 这与Li等[27]基于SMD模型预测多氯联苯KOW的结果一致，可能是因为MIDI!6D基组可以较为准确地描述电子分布[45]，从而提高预测准确性. SMD模型在参数化拟合的过程中，结合相同理论方法下，MIDI!6D基组比其它基组对含氟物质的溶剂化自由能预测误差相近或更小[26]，这可能是MIDI!6D基组表现最优的原因. 其它基组的结果表明，采用大基组计算能量，对提高PFASs的lgKOW预测准确性有限.
-
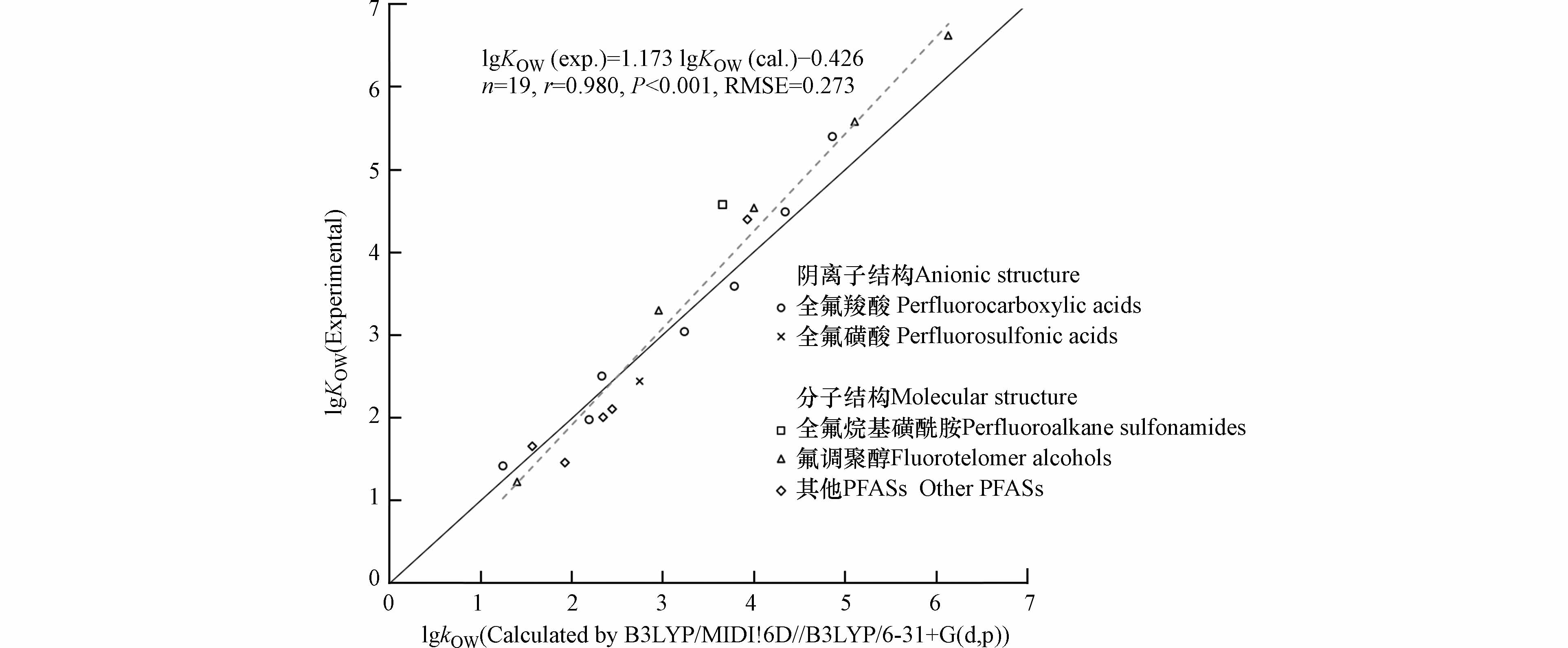
表3展示了不同方法预测准确性的排序，最优计算方法使用B3LYP/6-31+G（d,p）优化结构，使用B3LYP/MIDI!6D计算能量（以下简称为B3LYP/MIDI!6D//B3LYP/6-31+G（d,p））. 通过B3LYP/MIDI!6D//B3LYP/6-31+G（d,p）方法预测的lgKOW与实测值之间的r为0.980, RMSE为0.273，通过t检验，得到P < 0.001，说明该方法获得的预测值与实测值的回归模型在0.001的显著性水平上显著，具有统计学意义.
分别对8种阴离子形态和11种分子结构的PFASs的lgKOW计算值与实测值进行回归分析，发现无论阴离子形态还是分子形态，使用B3LYP/MIDI!6D//B3LYP/6-31+G（d,p）计算的lgKOW值与实测值的相关性最显著，对于阴离子形态：n = 8，r = 0.979, P < 0.001，RMSE = 0.269；对于分子形态：n = 11, r = 0.984，P < 0.001, RMSE = 0.475.
如图3所示，部分PFASs的lgKOW被低估，且预测值与实测值的差异有随着lgKOW递增的趋势，特别是对于lgKOW > 3的PFASs. 这可能是因为PFASs具有表面活性，在水中到达一定浓度以上时，往往会聚集成胶束或其他聚集体[50]. 在实验测量KOW中，PFASs的浓度相对较高，PFASs分子很有可能相互接触形成聚集体. PFASs的KOW实测值可能是单体或多聚体的混合值，而不是单个分子的实际值. PFASs的聚集体比单体分子更疏水[50 − 51]，因此，实验测定的表观KOW值可能高于基于单个分子的预测值. 一些PFASs的临界胶束浓度随着碳链长度的增加呈指数下降[50]，表面活性逐渐增强，这可能是导致分子量大的PFASs的lgKOW低估更严重的原因. 为获得与测试值具有一致性的lgKOW值，可根据下式预测：
前人基于SMD模型预测多氯联苯的lgKOW值的过程中，也发现对lgKOW低估的问题[27]. 由于多氯联苯具有π-π相互作用，易形成二聚体结构[52]，Li等[27]通过分析多氯联苯二聚体形式的影响，对结果进行了修正. 目前对于PFASs在溶剂中聚集体的具体形式尚不清楚[45, 53]，未来可以采用分子动力学模拟的手段，探究PFASs在水或辛醇相中的聚集行为，减少聚集体对lgKOW预测的影响.
表4列出了B3LYP/MIDI!6D//B3LYP/6-31+G（d,p）方法计算的∆GOW的分解结果，可见非静电能比静电能对∆GOW有更大的贡献，说明非极性作用是PFASs在正辛醇和水相间分配的主要作用. SMD模型计算的非静电能，由溶质排开溶剂形成空穴、溶质-溶剂色散相互作用以及溶质诱导的溶剂局部结构变化所引起的能量变化组成[26]，这3个过程对PFASs分配行为有重要影响. 从全氟羧酸和氟调聚醇的结果可以看出，两类PFASs的∆GOW中静电能相近，而非静电能部分的绝对值随着碳链长度和含氟原子数的增大而增大，说明碳链长度或含氟原子数是PFASs同系物中影响KOW的重要因素.
由表4可知，B3LYP/MIDI!6D//B3LYP/6-31+G（d,p）方法计算的lgKOW与实测值相近，残差绝对值在1以内. N-（2-羟乙基）-N-甲基全氟辛烷磺酰胺（MeFOSE）的lgKOW残差的绝对值较大. 如图4所示，全氟辛烷磺酸（PFOS）与MeFOSE结构类似，“尾部”都具有一条含8个碳原子的碳氟链. 然而，PFOS的lgKOW却比MeFOSE有着更小的残差绝对值，这可能由于它们“头部”结构的不同. PFOS的“头部”为磺基，而MeFOSE的“头部”为含氮基团. SMD模型在训练的过程中，对于含氮原子物质的溶剂化自由能预测结果表现较差[26]，预测误差高于平均值，这可能是MeFOSE的lgKOW预测结果残差较大的原因. 因此，当前基于SMD模型预测lgKOW的方法，应该慎重应用于含氮原子的化合物. 将来可以完善SMD模型的训练集，提高模型参数化效果，提升SMD模型对含不同元素的PFASs溶剂化自由能的计算准确性.
-
与以往PFASs的KOW预测模型及软件的结果相比（表5），本研究方法的RMSE较低，具有较高的预测准确性. Kim等[19]建立的QSAR模型的r和RMSE略优于本研究，但是其模型训练集中仅包含9种PFASs，且只涉及全氟羧酸和全氟磺酸，由于QSAR模型通常只适用于与训练集中物质具有相似结构的化合物，所以其应用域有限，而本研究预测的PFASs种类更多，可应用的范围更广.
-
如表6所示，基于筛选的最优方法，预测了其他没有实测值的PFASs的lgKOW，涉及全氟羧酸、全氟磺酸、全氟烷基磺酰胺、全氟烷基磺酰胺醇、全氟烷基磺酰胺乙酸、氟调聚羧酸和氟调聚磺酸.
-
本研究筛选了基于DFT结合SMD模型，预测PFASs的lgKOW方法. 得到最适合的方法是：使用B3LYP/6-31+G（d,p）优化几何结构，使用B3LYP/MIDI!6D计算能量. 发现PFASs溶剂化效应的非极性作用对PFASs的KOW起着重要影响. 基于所筛选的方法，为19种没有实测值的PFASs提供了lgKOW预测值. 与此前方法相比，本方法的预测准确性高，可预测PFASs的种类多. 本研究为填补PFASs的KOW缺失提供了方法支撑.
基于SMD模型预测全/多氟烷基化合物的正辛醇-水分配系数
Prediction of octanol-water partition coefficients of per- and polyfluoroalkyl substances based on SMD model
-
摘要: 全/多氟烷基化合物(PFASs)是备受关注的新污染物. 正辛醇-水分配系数(KOW)是评价化学品在环境中分配、迁移和归趋的重要参数，但大多数PFASs缺少KOW的实测值. 发展可靠的KOW预测方法，对填补PFASs的KOW数据缺失具有重要意义. 本研究通过基于溶质电子密度的溶剂化模型(SMD)描述溶剂化效应，以19种PFASs的lgKOW实测值为参照，从哈特里-福克自洽场和密度泛函理论与不同基组的组合中，筛选适于预测PFASs的lgKOW方法. 比较lgKOW实测值与不同方法所得预测值之间的相关系数(r)和均方根误差(RMSE)，发现当用B3LYP泛函结合6-31+G(d，p)基组优化几何结构，B3LYP泛函结合MIDI!6D基组计算能量时，预测效果最好(r = 0.980，P < 0.001，RMSE = 0.273). 发现溶剂形成空穴、溶质-溶剂色散作用和溶剂局部结构变化，为PFASs的KOW值的主要影响因素. 本研究为预测PFASs的KOW提供了一种可行的方法.
-
关键词:
- 全/多氟烷基化合物 /
- 正辛醇-水分配系数 /
- 哈特里-福克自洽场 /
- 密度泛函理论 /
- 基于溶质电子密度的溶剂化模型.
Abstract: Per- and polyfluoroalkyl substances (PFASs) are emerging pollutants with increasing concern. Octanol-water partition coefficient (KOW) is an important parameter for assessing the distribution, transport and fate of chemicals in the environment. However, most PFASs lack KOW values. It is of significance to develop a reliable method for predicting the KOW values of PFASs and filling the data gap. In this study, using the solvation model based on solute electron density (SMD) to mimic solvation effects and the experimental lgKOW data of 19 PFASs as references, a suitable method for predicting lgKOW values of PFASs was determined by evaluating the combination of Hartree-Fock self-consistent field and density functional theory with different basis-sets. Correlation coefficient (r) and root mean square error (RMSE) were adopted to compare the experimental and calculated lgKOW values from different methods. The optimum prediction results (r = 0.980, P < 0.001, RMSE = 0.273) were achieved using geometric structures optimized by the B3LYP functional with the 6-31+G(d,p) basis-set, and energy calculated using the B3LYP functional with the MIDI!6D basis-set. It was found that solvent cavitation, dispersion between the solute and solvent, and changes in local solvent structures are the main factors affecting the KOW values of PFASs. This study offers a feasible method for predicting the KOW values of PFASs. -
-
图 1 不同理论方法计算lgKOW值与实测值之间的r和RMSE值
Figure 1. Correlation coefficients （r） and root mean square errors （RMSE） between theoretically calculated and experimental lgKOW values
图 2 不同基组结合B3LYP泛函所计算的lgKOW与其实测值之间的r和RMSE值
Figure 2. Correlation coefficients （r） and root mean square errors （RMSE） between theoretically calculated and experimental lgKOW values
图 3 B3LYP/MIDI!6D//B3LYP/6-31+G（d,p）方法计算的lgKOW与实测值之间的回归曲线
Figure 3. Linear regression between experimental lgKOW and calculated values by B3LYP/MIDI!6D//B3LYP/6-31+G（d,p）
表 1 预测KOW的不同方法的原理及优缺点
Table 1. Principles, advantages and disadvantages of different methods for predicting KOW
预测方法
Prediction methods原理
Principles优点
Advantages缺点
DisadvantagesQSAR模型 相似结构的分子具有相似的性质. 对算力要求低 需要较多的训练数据 显式溶剂化模型 将溶剂分子作为独立的粒子，基于力场描述
溶质-溶剂的相互作用.结果相对准确，可以反映溶质-溶剂的相互作用 计算量大，计算采样复杂 隐式溶剂化模型 忽略溶剂分子的结构和分布，将溶剂描述为
均匀连续介质.与显示溶剂模型相比，计算速度较快 多数模型缺乏溶剂效应的极性与
非极性部分的定义
下载: 导出CSV
表 2 PFASs的lgKOW实测值
Table 2. Experimental lgKOW values of PFASs
中文名称
Chinese names英文名称
English names缩写
Abbreviation分子式
Molecular formulaCAS号
CAS number实测lgKOW
Experimental lgKOW全氟羧酸 Perfluorocarboxylic acids 全氟丁酸 Perfluorobutanoic acid PFBA C4HF7O2 375-22-4 1.43[30] 全氟戊酸 Perfluoropentanoic acid PFPeA C5HF9O2 2706-90-3 1.98[30] 全氟己酸 Perfluorohexanoic acid PFHxA C6HF11O2 307-24-4 2.51[30] 全氟庚酸 Perfluoroheptanoic acid PFHpA C7HF13O2 375-85-9 3.05[30] 全氟辛酸 Perfluorooctanoic acid PFOA C8HF15O2 335-67-1 3.60[30] 全氟壬酸 Perfluorononanoic acid PFNA C9HF17O2 375-95-1 4.50[31] 全氟癸酸 Perfluorodecanoic acid PFDA C10HF19O2 335-76-2 5.40[31] 全氟磺酸 Perfluorosulfonic acids 全氟辛烷磺酸 Perfluorooctane sulfonic acid PFOS C8HF17O3S 1763-23-1 2.45[32] 全氟烷基磺酰胺 Perfluoroalkane sulfonamides N-（2-羟乙基）-N-甲基全氟辛烷磺酰胺 N-Methyl Perfluorooctane sulfonamidoethanol MeFOSE C11H8F17NO3S 24448-09-7 4.58[33] 氟调聚醇 Fluorotelomer alcohols 2:1 氟调聚醇 2:1 Fluorotelomer alcohol 2:1 FTOH C3H3F5O 422-05-9 1.23[33] 4:2 氟调聚醇 4:2 Fluorotelomer alcohol 4:2 FTOH C6H5F9O 2043-47-2 3.30[34] 6:2 氟调聚醇 6:2 Fluorotelomer alcohol 6:2 FTOH C8H5F13O 647-42-7 4.54[34] 8:2 氟调聚醇 8:2 Fluorotelomer alcohol 8:2 FTOH C10H5F17O 678-39-7 5.58[34] 10:2 氟调聚醇 10:2 Fluorotelomer alcohol 10:2 FTOH C12H5F21O 865-86-1 6.63[34] 其他PFASs other PFASs 恩氟烷 Enflurane — C3H2ClF5O 13838-16-9 2.10[33] 六氟异丙醇 Hexafluoroisopropanol HFIP C3H2F6O 920-66-1 1.66[33] 全氟正戊烷 Perfluoropentane — C5F12 678-26-2 4.40[33] 六氟乙烷 Hexafluoroethane — C2F6 76-16-4 2.00[33] 六氟丙酮 Hexafluoroacetone — C3F6O 684-16-2 1.46[33]
下载: 导出CSV
表 3 PFASs的lgKOW预测准确性前10名的计算方法
Table 3. Top 10 calculation methods for prediction accuracy of lgKOW for PFASs
序号
Ordinal number几何优化
Geometry optimization能量计算
Energy calculationr RMSE 1 B3LYP/6-31+G（d,p） B3LYP/MIDI!6D 0.980 0.273 2 B3LYP/cc-pVTZ B3LYP/MIDI!6D 0.980 0.285 3 B3LYP/cc-pVTZ B3LYP/cc-pVTZ 0.979 0.294 4 B3LYP/6-31G（d,p） B3LYP/MIDI!6D 0.978 0.304 5 M062X/6-31+G（d,p） M062X/6-31+G（d,p） 0.978 0.304 6 B3LYP/6-31G（d） B3LYP/MIDI!6D 0.977 0.312 7 B3LYP/6-31+G（d,p） B3LYP/cc-pVTZ 0.977 0.312 8 M062X/6-31+G（d,p） M062X/MIDI!6D 0.977 0.312 9 M062X/6-31+G（d,p） M062X/cc-pVTZ 0.977 0.312 10 B3LYP/6-31G（d,p） B3LYP/cc-pVTZ 0.977 0.312
下载: 导出CSV
表 4 B3LYP/MIDI!6D//B3LYP/6-31+G（d,p）方法计算的∆GOW的静电能（
$ {{\Delta }\text{G}}_{\text{ENP}}^{\text{OW}} $ $ {{\Delta }\text{G}}_{\text{CDS}}^{\text{OW}} $ Table 4. Electrostatic （
$ {{\Delta }\text{G}}_{\text{ENP}}^{\text{OW}} $ $ {{\Delta }\text{G}}_{\text{CDS}}^{\text{OW}} $ PFASs名称
PFASs Name∆GOW/
（kcal·mol−1）$ {{\Delta }\text{G}}_{\text{ENP}}^{\text{OW}} $
（kcal·mol−1）$ {{\Delta }\text{G}}_{\text{CDS}}^{\text{OW}} $
（kcal·mol−1）lgKOW 预测值
Predicted values残差的绝对值
Absolute values of residuals全氟羧酸 全氟丁酸 −1.70 1.76 −3.46 1.24 0.19 全氟戊酸 −2.98 1.51 −4.49 2.18 0.20 全氟己酸 −3.16 1.77 −4.93 2.32 0.19 全氟庚酸 −4.41 1.57 −5.98 3.23 0.18 全氟辛酸 −5.15 1.60 −6.75 3.78 0.18 全氟壬酸 −5.92 1.58 −7.50 4.34 0.16 全氟癸酸 −6.63 1.61 −8.24 4.86 0.54 全氟磺酸 全氟辛烷磺酸 −3.74 1.61 −5.35 2.74 0.29 全氟烷基磺酰胺 N-（2-羟乙基）-N-甲基全氟辛烷磺酰胺 −4.97 2.48 −7.45 3.65 0.93 氟调聚醇 2:1 氟调聚醇 −1.91 1.49 −3.40 1.40 0.17 4:2 氟调聚醇 −4.02 1.40 −5.42 2.95 0.35 6:2 氟调聚醇 −5.46 1.46 −6.92 4.00 0.54 8:2 氟调聚醇 −6.95 1.50 −8.45 5.10 0.48 10:2 氟调聚醇 −8.37 1.54 −9.91 6.13 0.50 其他类PFASs 恩氟烷 −3.34 0.89 −4.23 2.44 0.34 六氟异丙醇 −2.15 1.35 −3.50 1.57 0.09 全氟正戊烷 −5.35 0.14 −5.49 3.92 0.48 六氟乙烷 −3.20 0.11 −3.31 2.34 0.34 六氟丙酮 −2.64 0.59 −3.23 1.93 0.47 注：残差代表预测值与实测值的差.
Note: residuals represent the difference between predicted values and experimental values.
下载: 导出CSV
表 5 B3LYP/MIDI!6D//B3LYP/6-31+G（d,p）方法与此前PFASs的lgKOW预测方法的比较
Table 5. Comparison of B3LYP/MIDI!6D//B3LYP/6-31+G（d,p） with previous prediction methods for lgKOW of PFASs
模型/软件
Model/Softwaren r RMSE 参考文献
ReferenceCOSMOthem 3 _ 0.502 Lampic等[54] EPI SuiteTM 3 _ 0.294 Lampic等[54] NICEATM 3 _ 1.133 Lampic等[54] OPERA 3 _ 0.283 Lampic等[54] pp-LFER 3 _ 0.362 Lampic等[54] SPARC 4 _ 0.861 Arp等[55] EPI SuiteTM 4 _ 1.271 Arp等[55] ClogP 4 _ 3.535 Arp等[55] COSMOtherm 4 - 1.659 Arp等[55] pp-LFER 6 _ 0.420 Endo和Goss[20] QSAR 9 0.994 0.155 Kim等[19] SMD 19 0.980 0.273 本研究 注：n代表模型或软件使用的实测数据个数.
Note: n represents the number of experimental data used by model or software.
下载: 导出CSV
表 6 B3LYP/MIDI!6D//B3LYP/6-31+G（d,p）方法预测的19种PFASs的lgKOW
Table 6. LgKOW values for 19 PFASs predicted by B3LYP/MIDI!6D//B3LYP/6-31+G（d,p）
中文名称
Chinese names英文名称
English names缩写
Abbreviation分子式
Molecular formulaCAS号
CAS number预测值
Predicted lgKOW全氟羧酸 Perfluorocarboxylic acids 全氟十二烷酸 Perfluorododecanoic acid PFDoDA C12HF23O2 307-55-1 5.91 全氟十三酸 Perfluorotridecanoic acid PFTrDA C13HF25O2 72629-94-8 6.46 全氟磺酸 Perfluorosulfonic acids 全氟戊烷磺酸 Perfluoropentane sulfonic acid PFPeS C5HF11O3S 2706-91-4 1.19 全氟己烷磺酸 Perfluorohexane sulfonic acid PFHxS C6HF13O3S 355-46-4 1.69 全氟庚烷磺酸 Perfluoroheptane sulfonic acid PFHpS C7HF15O3S 375-92-8 2.24 全氟壬烷磺酸 Perfluorononane sulfonic acid PFNS C9HF19O3S 68259-12-1 3.33 全氟癸烷磺酸 Perfluorodecane sulfonic acid PFDS C10HF21O3S 335-77-3 3.80 全氟烷基磺酰胺 Perfluoroalkane sulfonamides 全氟辛基磺酰胺 Perfluorooctane sulfonamide FOSA C8H2F17NO2S 754-91-6 3.00 N-甲基全氟辛烷磺酰胺 N-Methyl perfluorooctane sulfonamide MeFOSA C9H4F17NO2S 31506-32-8 3.64 全氟烷基磺酰胺醇 Perfluoroalkane sulfonamidoethanols 全氟辛烷磺酰胺乙醇 Perfluorooctane Sulfonamidoethanol FOSE C10H6F17NO3S 10116-92-4 2.94 N-乙基全氟辛基磺酰胺乙醇 N-Ethyl perfluorooctane sulfonamidoethanol EtFOSE C12H10F17NO3S 1691-99-2 3.96 全氟烷基磺酰胺乙酸 Perfluoroalkane sulfonamido acetic acids 全氟辛烷磺酰胺乙酸 Perfluorooctane sulfonamido acetic acid FOSAA C10H4F17NO4S 2806-24-8 2.23 2-（N-甲基全氟辛烷磺酰氨基）乙酸 N-Methyl perfluorooctane sulfonamido acetic acid MeFOSAA C11H6F17NO4S 2355-31-9 3.34 2-（N-乙基全氟辛烷磺酰氨基）乙酸 N-Ethyl perfluorooctane sulfonamido acetic acid EtFOSAA C12H8F17NO4S 2991-50-6 3.56 氟调聚羧酸 Fluorotelomer carboxylic acids 5:3氟调聚羧酸 5:3 Fluorotelomer carboxylic acid 5:3 FTCA C8H5F11O2 914637-49-3 3.27 6:2氟调聚羧酸 6:2 Fluorotelomer carboxylic acid 6:2 FTCA C8H3F13O2 53826-12-3 3.29 氟调聚磺酸 Fluorotelomer sulfonic acids 4:2氟调聚磺酸 4:2 Fluorotelomer sulfonic acid 4:2 FTSA C6H5F9O3S 757124-72-4 0.93 6:2氟调聚磺酸 6:2 Fluorotelomer sulfonic acid 6:2 FTSA C8H5F13O3S 27619-97-2 1.99 8:2氟调聚磺酸 8:2 Fluorotelomer sulfonic acid 8:2 FTSA C10H5F17O3S 39108-34-4 3.05
下载: 导出CSV
-
[1] OECD, Reconciling terminology of the universe of per- and polyfluoroalkyl substances: Recommendations and practical guidance [R]. OECD Series on Risk Management, No. 61, OECD Publishing, Paris, 2021. [2] KISSA E. Toxicology and environmental aspects in fluorinated surfactants and repellents [M]. 2nd ed. Marcel Dekker: New York, 2001, 97: 456-461. [3] YUE Y, FAN J Q, XIN G Q, et al. Comprehensive understanding of fluoroacetate dehalogenase-catalyzed degradation of fluorocarboxylic acids: A QM/MM approach[J]. Environmental Science & Technology, 2021, 55(14): 9817-9825. [4] YANG X H, LYAKURWA F, XIE H B, et al. Different binding mechanisms of neutral and anionic poly-/ perfluorinated chemicals to human transthyretin revealed by In silico models[J]. Chemosphere, 2017, 182: 574-583. doi: 10.1016/j.chemosphere.2017.05.016 [5] DU Z W, DENG S B, ZHANG S Y, et al. Selective and fast adsorption of perfluorooctanesulfonate from wastewater by magnetic fluorinated vermiculite[J]. Environmental Science & Technology, 2017, 51(14): 8027-8035. [6] SCHAIDER L A, BALAN S A, BLUM A, et al. Fluorinated compounds in U. S. fast food packaging[J]. Environmental Science & Technology Letters, 2017, 4(3): 105-111. [7] XIA C J, DIAMOND M L, PEASLEE G F, et al. Per- and polyfluoroalkyl substances in North American school uniforms[J]. Environmental Science & Technology, 2022, 56(19): 13845-13857. [8] U S EPA. PFAS master list of PFAS substances (Version 2) [DB/OL]. (2021-08-10). [2023-03-09] [9] LIU C, HATTON J, ARNOLD W A, et al. in situ sequestration of perfluoroalkyl substances using polymer-stabilized powdered activated carbon[J]. Environmental Science & Technology, 2020, 54(11): 6929-6936. [10] LAN Z H, YAO Y M, XU J Y, et al. Novel and legacy per- and polyfluoroalkyl substances (PFASs) in a farmland environment: Soil distribution and biomonitoring with plant leaves and locusts[J]. Environmental Pollution, 2020, 263: 114487. doi: 10.1016/j.envpol.2020.114487 [11] TIAN Y, YAO Y M, CHANG S A, et al. Occurrence and phase distribution of neutral and ionizable per- and polyfluoroalkyl substances (PFASs) in the atmosphere and plant leaves around landfills: A case study in Tianjin, China[J]. Environmental Science & Technology, 2018, 52(3): 1301-1310. [12] WANG B, YAO Y M, WANG Y, et al. Per- and polyfluoroalkyl substances in outdoor and indoor dust from mainland China: Contributions of unknown precursors and implications for human exposure[J]. Environmental Science & Technology, 2022, 56(10): 6036-6045. [13] CHEN Z H, YANG T Y, WALKER D I, et al. Dysregulated lipid and fatty acid metabolism link perfluoroalkyl substances exposure and impaired glucose metabolism in young adults[J]. Environment International, 2020, 145: 106091. doi: 10.1016/j.envint.2020.106091 [14] DING N, HARLOW S, JOHN F RANDOLPH J Jr, et al. Perfluoroalkyl and polyfluoroalkyl substances (PFAS) and their effects on the ovary[J]. Human Reproduction Update, 2020, 26: 724-752. doi: 10.1093/humupd/dmaa018 [15] BLAKE B E, PINNEY S M, HINES E P, et al. Associations between longitudinal serum perfluoroalkyl substance (PFAS) levels and measures of thyroid hormone, kidney function, and body mass index in the Fernald Community Cohort[J]. Environmental Pollution, 2018, 242: 894-904. doi: 10.1016/j.envpol.2018.07.042 [16] AMÉZQUETA S, SUBIRATS X, FUGUET E, et al. Octanol-water partition constant[M]//Liquid-Phase Extraction. Amsterdam: Elsevier, 2020: 183-208. [17] LI M, LI J, LU Y C, et al. Developing the QSPR model for predicting the storage lipid/water distribution coefficient of organic compounds[J]. Frontiers of Environmental Science & Engineering, 2020, 15(2): 1-8. [18] COSTANZA J, ABRIOLA L M, PENNELL K D. Aqueous film-forming foams exhibit greater interfacial activity than PFOA, PFOS, or FOSA[J]. Environmental Science & Technology, 2020, 54(21): 13590-13597. [19] KIM M, LI L Y, GRACE J R, et al. Selecting reliable physicochemical properties of perfluoroalkyl and polyfluoroalkyl substances (PFASs) based on molecular descriptors[J]. Environmental Pollution, 2015, 196: 462-472. doi: 10.1016/j.envpol.2014.11.008 [20] ENDO S, GOSS K U. Predicting partition coefficients of polyfluorinated and organosilicon compounds using polyparameter linear free energy relationships (PP-LFERs)[J]. Environmental Science & Technology, 2014, 48(5): 2776-2784. [21] STEINMANN S N, SAUTET P, MICHEL C. Solvation free energies for periodic surfaces: Comparison of implicit and explicit solvation models[J]. Physical Chemistry Chemical Physics, 2016, 18(46): 31850-31861. doi: 10.1039/C6CP04094B [22] NEDYALKOVA M A, MADURGA S, TOBISZEWSKI M, et al. Calculating the partition coefficients of organic solvents in octanol/water and octanol/air[J]. Journal of Chemical Information and Modeling, 2019, 59(5): 2257-2263. doi: 10.1021/acs.jcim.9b00212 [23] GUAN D, LUI R, MATTHEWS S. LogP prediction performance with the SMD solvation model and the M06 density functional family for SAMPL6 blind prediction challenge molecules[J]. Journal of Computer-Aided Molecular Design, 2020, 34(5): 511-522. doi: 10.1007/s10822-020-00278-1 [24] KUNDI V, HO J. Predicting octanol–water partition coefficients: Are quantum mechanical implicit solvent models better than empirical fragment-based methods?[J]. The Journal of Physical Chemistry B, 2019, 123(31): 6810-6822. doi: 10.1021/acs.jpcb.9b04061 [25] KLAMT A. The COSMO and COSMO-RS solvation models[J]. Wiley Interdisciplinary Reviews: Computational Molecular Science, 2018, 8(1): e1338. [26] MARENICH A V, CRAMER C J, TRUHLAR D G. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions[J]. The Journal of Physical Chemistry B, 2009, 113(18): 6378-6396. doi: 10.1021/jp810292n [27] LI W R, SONG G B, ZHANG J, et al. Estimation of octanol-water partition coefficients of PCBs based on the solvation free energy[J]. Computational and Theoretical Chemistry, 2021, 1202: 113324. doi: 10.1016/j.comptc.2021.113324 [28] ITRC. Per- and polyfluoroalkyl substances technical and regulatory guidance [EB/OL]. [2023-04-09]. [29] DING G H, PEIJNENBURG W J G M. Physicochemical properties and aquatic toxicity of poly- and perfluorinated compounds[J]. Critical Reviews in Environmental Science and Technology, 2013, 43(6): 598-678. doi: 10.1080/10643389.2011.627016 [30] IWAI H, TSUDA N. Ecotox findings for ammonium perfluorohexanoate [EB/OL]. (2011-06-07). [2023-03-09] [31] KELLY B C, IKONOMOU M G, BLAIR J D, et al. Perfluoroalkyl contaminants in an Arctic marine food web: Trophic magnification and wildlife exposure[J]. Environmental Science & Technology, 2009, 43(11): 4037-4043. [32] JING P, RODGERS P J, AMEMIYA S. High lipophilicity of perfluoroalkyl carboxylate and sulfonate: Implications for their membrane permeability[J]. Journal of the American Chemical Society, 2009, 131(6): 2290-2296. doi: 10.1021/ja807961s [33] WILLIAMS A J, GRULKE C M, EDWARDS J, et al. The CompTox Chemistry Dashboard: A community data resource for environmental chemistry[J]. Journal of Cheminformatics, 2017, 9(1): 1-27. doi: 10.1186/s13321-016-0187-6 [34] CARMOSINI N, LEE L S. Partitioning of fluorotelomer alcohols to octanol and different sources of dissolved organic carbon[J]. Environmental Science & Technology, 2008, 42(17): 6559-6565. [35] FRISCH M J, TRUCKS G W, SCHLEGEL H B, et al. Gaussian 09, Revision D. 01 [CP]. Gaussian, Inc. , Wallingford CT, 2013. [36] DENNINGTON R, KEITH T, MILLAM J. GaussView, Version 6 [CP]. Semichem Inc. , Shawnee Mission, KS, 2016. [37] LEVINE I N. Quantum chemistry [M]. 3rd ed. New Jersey: Allyn and Bacon, Inc. , 1983: 11-20. [38] STEPHENS P J, DEVLIN F J, CHABALOWSKI C F, et al. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields[J]. The Journal of Physical Chemistry, 1994, 98(45): 11623-11627. doi: 10.1021/j100096a001 [39] ZHAO Y, SCHULTZ N E, TRUHLAR D G. Design of density functionals by combining the method of constraint satisfaction with parametrization for thermochemistry, thermochemical kinetics, and noncovalent interactions[J]. Journal of Chemical Theory and Computation, 2006, 2(2): 364-382. doi: 10.1021/ct0502763 [40] ZHAO Y, TRUHLAR D. Density functionals with broad applicability in chemistry[J]. Accounts of Chemical Research, 2008, 41(2): 157-167. doi: 10.1021/ar700111a [41] PETERSSON G A, BENNETT A, TENSFELDT T G, et al. A complete basis set model chemistry. I. The total energies of closed-shell atoms and hydrides of the first-row elements[J]. The Journal of Chemical Physics, 1988, 89(4): 2193-2218. doi: 10.1063/1.455064 [42] PETERSSON G A, AL-LAHAM M A. A complete basis set model chemistry. II. Open-shell systems and the total energies of the first-row atoms[J]. The Journal of Chemical Physics, 1991, 94(9): 6081-6090. doi: 10.1063/1.460447 [43] CLARK T, CHANDRASEKHAR J, SPITZNAGEL G W, et al. Efficient diffuse function-augmented basis sets for anion calculations. III. The 3-21+G basis set for first-row elements, Li-F[J]. Journal of Computational Chemistry, 1983, 4(3): 294-301. doi: 10.1002/jcc.540040303 [44] KENDALL R A, DUNNING T H Jr, HARRISON R J. Electron affinities of the first-row atoms revisited. Systematic basis sets and wave functions[J]. The Journal of Chemical Physics, 1992, 96(9): 6796-6806. doi: 10.1063/1.462569 [45] EASTON R E, GIESEN D J, WELCH A, et al. The MIDI!basis set for quantum mechanical calculations of molecular geometries and partial charges[J]. Theoretica Chimica Acta, 1996, 93(5): 281-301. doi: 10.1007/BF01127507 [46] HO J, KLAMT A, COOTE M L. Comment on the correct use of continuum solvent models[J]. The Journal of Physical Chemistry A, 2010, 114(51): 13442-13444. doi: 10.1021/jp107136j [47] TIRADO-RIVES J, JORGENSEN W L. Performance of B3LYP density functional methods for a large set of organic molecules[J]. Journal of Chemical Theory and Computation, 2008, 4(2): 297-306. doi: 10.1021/ct700248k [48] HOHENSTEIN E G, CHILL S T, SHERRILL C D. Assessment of the performance of the M05–2X and M06–2X exchange-correlation functionals for noncovalent interactions in biomolecules[J]. Journal of Chemical Theory and Computation, 2008, 4(12): 1996-2000. doi: 10.1021/ct800308k [49] TENTSCHER P R, AREY J S. Geometries and vibrational frequencies of small radicals: Performance of coupled cluster and more approximate methods[J]. Journal of Chemical Theory and Computation, 2012, 8(6): 2165-2179. doi: 10.1021/ct300194x [50] KRAFFT M P, RIESS J G. Selected physicochemical aspects of poly- and perfluoroalkylated substances relevant to performance, environment and sustainability—Part one[J]. Chemosphere, 2015, 129: 4-19. doi: 10.1016/j.chemosphere.2014.08.039 [51] LI W R, DING G H, GAO H, et al. Prediction of octanol-air partition coefficients for PCBs at different ambient temperatures based on the solvation free energy and the dimer ratio[J]. Chemosphere, 2020, 242: 125246. doi: 10.1016/j.chemosphere.2019.125246 [52] HWANG J, DIAL B E, LI P, et al. How important are dispersion interactions to the strength of aromatic stacking interactions in solution?[J]. Chemical Science, 2015, 6(7): 4358-4364. doi: 10.1039/C5SC01370D [53] BHHATARAI B, GRAMATICA P. Prediction of aqueous solubility, vapor pressure and critical micelle concentration for aquatic partitioning of perfluorinated chemicals[J]. Environmental Science & Technology, 2011, 45(19): 8120-8128. [54] LAMPIC A, PARNIS J M. Property estimation of per- and polyfluoroalkyl substances: A comparative assessment of estimation methods[J]. Environmental Toxicology and Chemistry, 2020, 39(4): 775-786. doi: 10.1002/etc.4681 [55] ARP H P H, NIEDERER C, GOSS K U. Predicting the partitioning behavior of various highly fluorinated compounds[J]. Environmental Science & Technology, 2006, 40(23): 7298-7304. -
点击查看大图
图( 4) 表( 6)
计量
- 文章访问数: 1857
- HTML全文浏览数: 1857
- PDF下载数: 55
- 施引文献: 0
